题目内容
已知α、β∈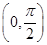
，sinα＝
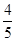，tan(α－β)＝－
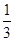，求cosβ的值．
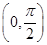，sinα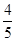＝，tan(α－β)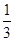＝－，求cosβ的值．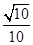
∵ α、β∈，∴ －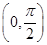
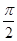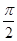＜α－β＜.又tan(α－β)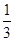＝－＜0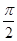，∴ －＜α－β＜0.
∴
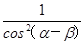＝1＋tan2(α－β)＝
.
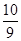∴ cos(α－β)＝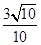
，sin(α－β)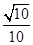＝－.又sinα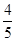＝，∴ cosα＝
.
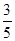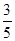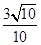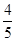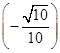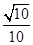
∴ cosβ＝cos[α－(α－β)]＝cosαcos(α－β)＋sinαsin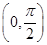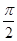(α－β)＝×＋×
＝
，∴ －＜α－β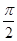＜.又tan(α－β)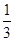＝－＜0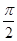，∴ －＜α－β＜0.∴
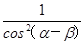＝1＋tan2(α－β)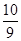＝.∴ cos(α－β)＝
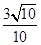，sin(α－β)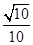＝－.又sinα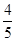＝，∴ cosα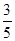＝.∴ cosβ＝cos[α－(α－β)]＝cosαcos(α－β)＋sinαsin(α－β)＝
×＋×＝
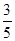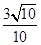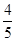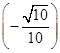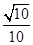
练习册系列答案
阅读快车系列答案
相关题目
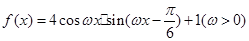的最小正周期是
．
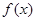的单调递增区间；
，
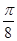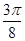]上的最大值和最小值．
＝
，
π＜x＜
π，求
的值．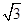
[tan(18°－x)＋tan(12°＋x)]＝________．
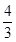，sin(α＋β)＝
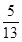，其中α，β∈(0，π)，则sin α的值为________．
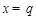时，函数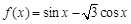
取得最大值，则
. 
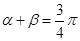，则
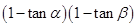的值为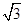 
)·sin40°.
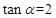，那么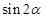
的值是（ ）
