数列{an}满足:a1=2,an=1.则a4= ,若{an}有一个形如an=Asin+b的通项公式.其中A,b,ω,φ均为实数.且A＞0.ω＞0.|φ|＜.则此通项公式可以为an= . 题目和参考答案——青夏教育精英家教网—

题目内容

数列{a_n}满足：a₁=2,a_n=1(n=2,3,4,…)，则a₄=___________；若{a_n}有一个形如a_n=Asin(ωn+φ)+b的通项公式，其中A,b,ω,φ均为实数，且A＞0，ω＞0，|φ|＜，则此通项公式可以为a_n=___________.（写出一个即可）

2 a_n=3sin(n-)+.a₁=2,a_n=1,∴a₂=1=,a₃=1-2=-1,a₄=1+1=2.

∵a₁=a₄,∴T=3.∴=3.∴ω=.∴a_n=Asin(n+φ)+b.∵a₁=2,a₂=,a₃=-1,

∴

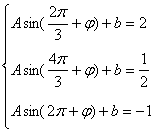
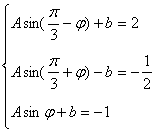
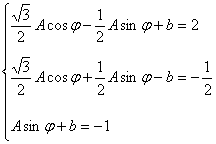
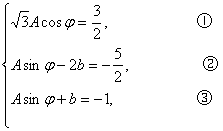
由②③消去Asinφ,得b=，∴Asinφ=-.④

得tanφ=-,∵|φ|＜,∴φ=-.

∴sinφ=.∴A=.

∴a_n=3sin(n-)+.

练习册系列答案

，bn=n(1-an)(n∈N*)，求数列{b_n}的前n项和S_n．

数列{a_n}满足a₁=a，an+1=

an+3

，n=1，2，3，…．
（Ⅰ）若a_n+1=a_n，求a的值；
（Ⅱ）当a=

时，证明：an＜

；
（Ⅲ）设数列{a_n-1}的前n项之积为T_n．若对任意正整数n，总有（a_n+1）T_n≤6成立，求a的取值范围．

（2011•天津模拟）设数列{a_n}满足a₁=a，a_n+1=ca_n+1-c（n∈N^*），其中a，c为实数，且c≠0．
（1）求证：a≠1时数列{a_n-1}是等比数列，并求a_n；
（2）设a=

，bn=n(1-an)(n∈N*)，求数列{b_n}的前n项和S_n；
（3）设a=

(n∈N*)，记dn=c2n-c2n-1(n∈N*)，设数列{d_n}的前n项和为T_n，求证：对任意正整数n都有Tn＜

．

（2009•大连二模）已知a为实数，数列{a_n}满足a₁=a，当n≥2时，an=

an-1-4 (an-1＞4)

5-an-1 (an-1≤4)

（I）当a=200时，填写下列表格；

N	2	3	51	200
a_n

（II）当a=200时，求数列{a_n}的前200项的和S₂₀₀；
（III）令b n=

(-2)n

，T_n=b₁+b₂…+b_n求证：当1＜a＜

)（n∈N^*）
（1）求数列{a_n}的通项公式；
（2）若a=8b，且等比数列{b_n}同时满足：①b₁=a₁，b₂=a₅；②数列{b_n}的每一项都是数列{a_n}中的某一项．试判断数列{b_n}是有穷数列或是无穷数列，并简要说明理由；
（3）对问题（2）继续探究，若b₂=a_m（m＞1，m是常数），当m取何正整数时，数列{b_n}是有穷数列；当m取何正整数时，数列{b_n}是无穷数列，并说明理由．

试题分类