题目内容
【题目】已知函数y=![]() (n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
(n∈Z)的图像与两坐标轴都无公共点,且其图像关于y轴对称,求n的值,并画出函数图像.
【答案】n=-1或n=1或n=3,此时解析式为y=x0(x≠0)或y=x-4(x≠0),图像见解析
【解析】试题分析:由题意可得,可得幂指数![]() 为负数,可得
为负数,可得![]() ,且为偶数,讨论
,且为偶数,讨论 ![]() 时,幂指数
时,幂指数![]() 是否为偶数,可得
是否为偶数,可得![]() 合题意,分别代入可得函数的解析式,从而得到函数的图象.
合题意,分别代入可得函数的解析式,从而得到函数的图象.
试题解析:因为图像与x轴无交点,所以n2-2n-3≤0,又图像关于y轴对称,则n2-2n-3为偶数.
由n2-2n-3≤0,得-1≤n≤3,又n∈Z,所以n=0,±1,2,3.
当n=0时,n2-2n-3=-3不是偶数;
当n=1时,n2-2n-3=-4是偶数;
当n=-1时,n2-2n-3=0是偶数;
当n=2时,n2-2n-3=-3不是偶数;
当n=3时,n2-2n-3=0是偶数.
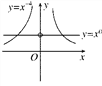
综上,n=-1或n=1或n=3,此时解析式为y=x0(x≠0)或y=x-4(x≠0),如图.

练习册系列答案
相关题目
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附: ![]()