题目内容
已知函数f(x)的定义域为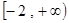 ,部分对应值如下表,
,部分对应值如下表,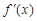 为f (x)的导函数,函数
为f (x)的导函数,函数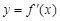 的图象如右图所示,若两正数a,b满足
的图象如右图所示,若两正数a,b满足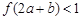 ,则
,则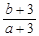 的取值范围是
的取值范围是
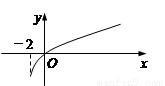
【答案】
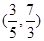
【解析】略

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
已知函数f(x)的定义域为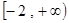 ,部分对应值如下表,
,部分对应值如下表,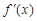 为f (x)的导函数,函数
为f (x)的导函数,函数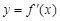 的图象如右图所示,若两正数a,b满足
的图象如右图所示,若两正数a,b满足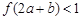 ,则
,则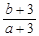 的取值范围是
的取值范围是
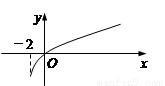
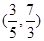
【解析】略

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案