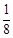题目内容
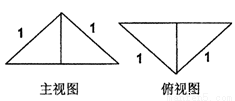
把边长为1的正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,形成三棱锥C-ABD的正视图与俯视图如图所示,则侧视图的面积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据三棱锥的正视图和俯视图确定三棱锥的侧视图,根据侧视图的结构计算面积即可.
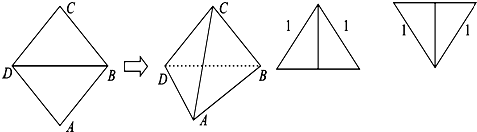
解答:解: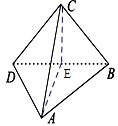 取BD的中点E,连结CE,AE,
取BD的中点E,连结CE,AE,
∵平面ABD⊥平面CBD,
∴CE⊥AE,
∴三角形直角△CEA是三棱锥的侧视图,
∵BD=
,∴CE=AE=
,
∴△CEA的面积S=
×
×
=
,
故选:B.
 取BD的中点E,连结CE,AE,
取BD的中点E,连结CE,AE,∵平面ABD⊥平面CBD,
∴CE⊥AE,
∴三角形直角△CEA是三棱锥的侧视图,
∵BD=
| 2 |
| ||
| 2 |
∴△CEA的面积S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
故选:B.
点评:本题主要考查三视图的识别和应用,根据三棱锥的结构得到三棱锥的侧视图是解决本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
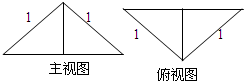 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥C-ABD的主视图与俯视图如图所示,则左视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥C-ABD的主视图与俯视图如图所示,则左视图的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
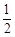 B.
B.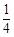 C.
C.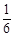 D.
D.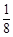
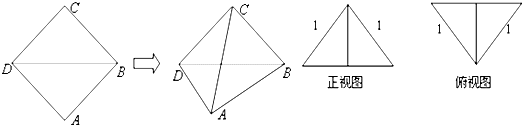
 沿对角线
沿对角线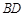 折起形成三棱锥
折起形成三棱锥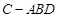 的主视图与俯视图如图所示,则左视图的面积为(
)
的主视图与俯视图如图所示,则左视图的面积为(
)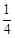 B.
B.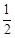
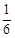 D.
D.