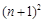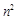题目内容
(本题满分12分)设数列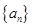 的前
的前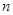 项和为
项和为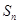 ,满足
,满足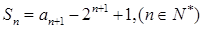 ,且
,且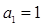 。
。
(Ⅰ)求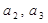 的值;
的值;
(Ⅱ)求数列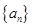 的通项公式;
的通项公式;
(Ⅲ)设数列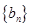 的前
的前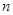 项和为
项和为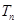 ,且
,且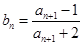 ,证明:对一切正整数
,证明:对一切正整数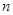 , 都有:
, 都有: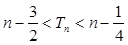
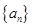 的前
的前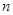 项和为
项和为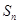 ,满足
,满足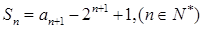 ,且
,且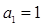 。
。(Ⅰ)求
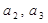 的值;
的值;(Ⅱ)求数列
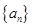 的通项公式;
的通项公式;(Ⅲ)设数列
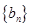 的前
的前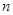 项和为
项和为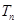 ,且
,且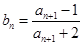 ,证明:对一切正整数
,证明:对一切正整数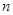 , 都有:
, 都有: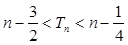
(Ⅰ)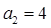 ,
,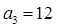 ;(Ⅱ)
;(Ⅱ)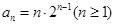
(Ⅲ)利用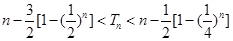 ,推出
,推出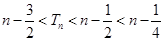 。
。
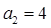 ,
,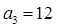 ;(Ⅱ)
;(Ⅱ)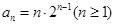
(Ⅲ)利用
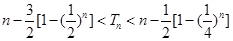 ,推出
,推出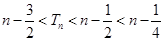 。
。试题分析:(Ⅰ)∵
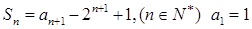
∴
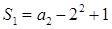
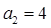
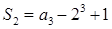
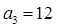 …………………………………4分
…………………………………4分(Ⅱ)由
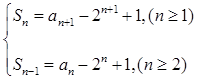 得
得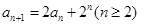
检验知
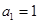 ,
,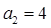 满足
满足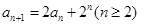
∴
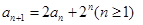
变形可得
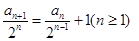
∴数列
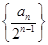 是以1为首项,1为公差的等差
是以1为首项,1为公差的等差 解得
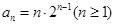 …………………………………………………7分
…………………………………………………7分(Ⅲ)由(Ⅱ)知
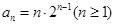
代入得
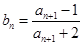 =
=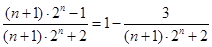 ……………8分
……………8分∵
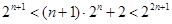
∴
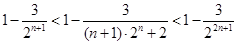
∴

∴
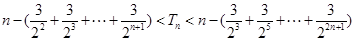
即

∴
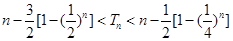
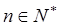 ∴
∴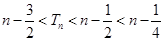 …………………………………………………12分
…………………………………………………12分点评:典型题,本题首先由
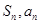 的故选,确定数列的通项公式是关键。不等式证明中运用了“放缩法”,本题较难。
的故选,确定数列的通项公式是关键。不等式证明中运用了“放缩法”,本题较难。
练习册系列答案
相关题目
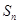 是数列{
是数列{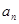 }的前n项和,
}的前n项和, ,那么数列{
,那么数列{ 中,
中, 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且 公比
公比
 满足:
满足: 的前n项和
的前n项和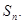
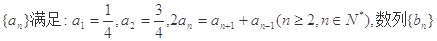 满足:
满足: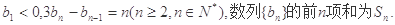
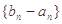 为等比数列;
为等比数列;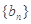 为递增数列;
为递增数列; 的取值范围。
的取值范围。 中,每 行 中 的 三 个 数 成 等 差 数 列,且
中,每 行 中 的 三 个 数 成 等 差 数 列,且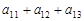 、
、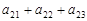 、
、 成等比数列,下列四个判断正确的有 (A )
成等比数列,下列四个判断正确的有 (A ) 必成等比数列 ②第1列
必成等比数列 ②第1列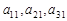 不一定成等比数列
不一定成等比数列 ④若9个数之和等于9,则
④若9个数之和等于9,则
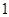 和
和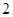 之间插入
之间插入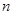 个实数,使得这
个实数,使得这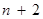 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这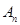 ,令
,令 ,
,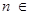 N
N .
.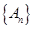 的前
的前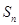 ;
;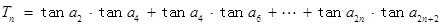 .
. 的公比为
的公比为 ,前n项和
,前n项和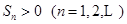 。
。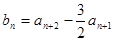 ,记
,记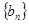 的前n项和为
的前n项和为 ,试比较
,试比较 与
与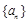 满足
满足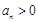 ,
,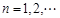 ,且
,且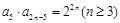 ,且当
,且当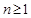 时,
时, ( )
( )