题目内容
21.如图,椭圆Q:![]() =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
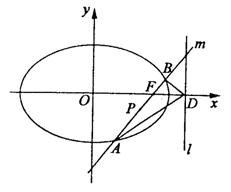
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
).确定θ的值,使原点距椭圆Q的右准线l最远.此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
解:如图,

(1)设椭圆Q:![]() =1上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
=1上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
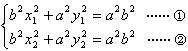
1°当AB不垂直x轴时,x1≠x2,
由①-②得
b2(x1-x2)2x+a2(y1-y2)2y=0,
∴![]()
∴b2x2+a2y2-b2cx=0, ……………(*)
2°当AB垂直于x轴时,点P即为点F,满足方程(*).
故所求点P的轨迹H的方程为:b2x2+a2y2-b2cx=0.
(2)因为,椭圆Q右准线l方程是x=![]() ,原点距椭圆Q的右准线l的距离为
,原点距椭圆Q的右准线l的距离为![]() ,
,
由于c2=a2-b2,a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).
).
则![]() =
=![]() .
.
当θ=![]() 时,上式达到最大值,所以当θ=
时,上式达到最大值,所以当θ=![]() 时,原点距椭圆Q的右准线l最远.
时,原点距椭圆Q的右准线l最远.
此时a2=2,b2=1,c=1,D(2,0),|DF|=1.
设椭圆Q:![]() =1上的点A(x1,y1)、B(x2,y2),
=1上的点A(x1,y1)、B(x2,y2),
△ABD面积S=![]() |y1|+
|y1|+![]() |y2|=
|y2|=![]() |y1-y2|.
|y1-y2|.
设直线m的方程为x=ky+1,代入![]() =1中,得(2+k2)y2+2ky-1=0.
=1中,得(2+k2)y2+2ky-1=0.
由韦达定理得y1+y2=-![]() ,y1y2=-
,y1y2=-![]() ,
,
4S2=(y1-y2)2=(y1+y2)2-4y1y2=![]() ,
,
令t=k2+1≥1,得4S2≤![]() =2,当t=1,k=0取等号.
=2,当t=1,k=0取等号.
因此,当直线m绕点F转动到垂直x轴位置时,三角形ABD的面积最大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
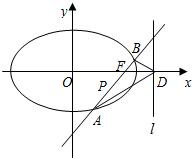 如图,椭圆
如图,椭圆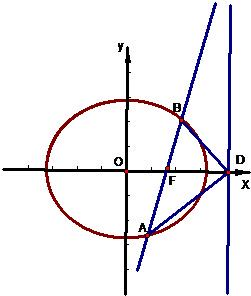 如图,椭圆Q:
如图,椭圆Q:
