题目内容
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR },B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求实数a的取值范围.
,求实数a的取值范围.
(1)A={x| a–2<x<a+2};B={x|–2<x<3}.(2)0≤a≤1.
解析试题分析:(1) 由| x–a | < 2,得a–2<x<a+2,所以A={x| a–2<x<a+2}………………………3分
由 <1,得
<1,得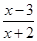 <0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
<0,即 –2<x<3,所以B={x|–2<x<3}.…………………………6分
(2) 若AÍB,所以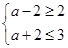 ,…………………………………………………………10分
,…………………………………………………………10分
所以0≤a≤1.………………………………………………………………………………12分
考点:含绝对值的不等式的解法;分式不等式的解法;集合间的关系。
点评:解分式不等式的主要步骤是:移项—通分—分式化整式。属于基础题型。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 ,集合
,集合 .
. ,求
,求 解析式。
解析式。 ,且
,且 时的最小值为
时的最小值为 ,求实数
,求实数 的值。
的值。 ,
, ,
,  .
. ;
; 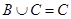 ,求实数
,求实数 的取值范围.
的取值范围. ,集合
,集合 ,
, ,
,
 ,
, ;(2)若
;(2)若 ,求
,求 的取值范围.
的取值范围. ,B=
,B= ,
, 时,求
时,求
 :
: ,
, :
: ,且
,且 的取值范围。
的取值范围。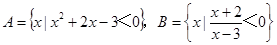
 是
是 上的增函数,且过
上的增函数,且过 和
和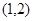 两点,集合
两点,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为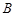 .
. 成立的实数
成立的实数 的取值范围.
的取值范围. ,
,
 ,求
,求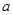 的值;
的值; ,求
,求 ,
, ,
, ,
, .
. ; (2)若
; (2)若 ,求实数
,求实数 的取值范围.
的取值范围.