题目内容
【题目】已知函数f(x)=ax2-2x+1.
(1)当![]() ,试讨论函数f(x)的单调性;
,试讨论函数f(x)的单调性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
(3)在(2)的条件下,求g(a)的最小值.
【答案】(1) ![]() 时增区间
时增区间![]() ,减区间
,减区间![]() ,
,![]() 时增区间
时增区间![]() ,减区间
,减区间![]()
(2) 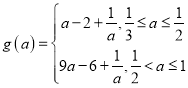 (3)
(3) ![]()
【解析】
试题分析:(1)通过讨论a的符合,结合二次函数的性质,从而判断出函数的单调性;(2)通过讨论a的范围,求出f(x)的单调区间,从而求出函数的最值,进而求出g(a)的解析式;(3)根据a的范围,求出g(a)的单调性,从而求出g(a)的最小值
试题解析:(1)![]()
![]() -----2分
-----2分
(2)∵![]() ≤a≤1,∴f(x)的图象为开口向上的抛物线,且对称轴为x=
≤a≤1,∴f(x)的图象为开口向上的抛物线,且对称轴为x=![]() ∈[1,3].
∈[1,3].
∴f(x)有最小值N(a)=1-![]() .
.
当2≤![]() ≤3时,a∈[
≤3时,a∈[![]() ,
,![]() ],f(x)有最大值M(a)=f(1)
],f(x)有最大值M(a)=f(1)
=a-1;
当1≤![]() <2时,a∈(
<2时,a∈(![]() ,1],f(x)有最大值M(a)=f(3)
,1],f(x)有最大值M(a)=f(3)
=9a-5;
∴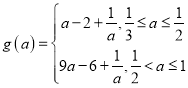 -----7分
-----7分
(3)设![]() ≤a1<a2≤
≤a1<a2≤![]() ,则g(a1)-g(a2)=(a1-a2)(1-
,则g(a1)-g(a2)=(a1-a2)(1-![]() )>0,
)>0,
∴g(a1)>g(a2),∴g(a)在[![]() ,
,![]() ]上是减函数.
]上是减函数.
设![]() <a1<a2≤1,则g(a1)-g(a2)=(a1-a2)(9-
<a1<a2≤1,则g(a1)-g(a2)=(a1-a2)(9-![]() )<0,∴g(a1)<g(a2),
)<0,∴g(a1)<g(a2),
∴g(a)在(![]() ,1]上是增函数.
,1]上是增函数.
∴当a=![]() 时,g(a)有最小值
时,g(a)有最小值![]() . -----12分
. -----12分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
