题目内容
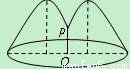
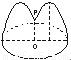
如图，花坛水池中央有一喷泉，水管OP =1 m，水从喷头P喷出后呈抛物线状，先向上至最高点后落下，若最高点距水面2 m，P距抛物线的对称轴1 m，则水池的直径至少应设计多少米(精确到整数位)?
思路解析：这一应用问题用解析几何的方法求解，应体现解析几何的基本思想，建坐标系后，利用解析法求出水池的半径即可.
解：如图所示，建立坐标系，设抛物线方程为x2＝-2py(p＞0)，依题意有P′(1，-1)在此抛物线上，代入得p＝
，故得抛物线方程为x2＝-y.又B在抛物线上，将B(x，-2)代入抛物线方程得x=
，即|AB|＝
，则水池半径应为|AB|+1＝
+1,因此所求水池的直径为2(1+
)，约为5 m，即水池的直径至少应设计为5 m.
练习册系列答案
相关题目
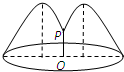如图，花坛水池中央有一喷泉，水管OP=1m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面2m，P距抛物线对称轴1m，则在水池直径的下列可选值中，最合算的是（ ）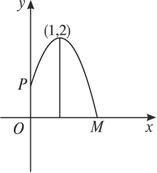
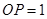米，水从喷头
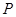喷出后呈抛物线状，先向上至最高点后落下，如果最高点距离水面2米，
