题目内容
已知平面上的动点P(x,y)及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是 k1,k2且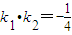 .
.(1)求动点P的轨迹C的方程;
(2)设直线l:y=kx+m与曲线C交于不同的两点M,N.
①若OM⊥ON(O为坐标原点),证明点O到直线l的距离为定值,并求出这个定值
②若直线BM,BN的斜率都存在并满足
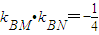 ,证明直线l过定点,并求出这个定点.
,证明直线l过定点,并求出这个定点.
【答案】分析:(1)利用斜率计算公式即可得出;
(2)把直线l的方程与椭圆方程联立得到根与系数的关系,①利用OM⊥ON?x1x2+y1y2=0即可得到k与m的关系,再利用点到直线的距离公式即可证明;
②利用斜率计算公式和根与系数的关系即可得出k与m的关系,进而证明结论.
解答:解:(1)由题意得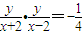 ,(x≠±2),即x2+4y2=4(x≠±2).
,(x≠±2),即x2+4y2=4(x≠±2).
∴动点P的轨迹C的方程是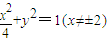 .
.
(2)设点M(x1,y1),N(x2,y2),联立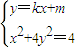 ,化为(1+4k2)x2+8kmx+4m2-4=0,
,化为(1+4k2)x2+8kmx+4m2-4=0,
∴△=64k2m2-16(m2-1)(1+4k2)=16(1+4k2-m2)>0.
∴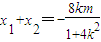 ,
,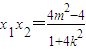 .
.
∴y1y2=(kx1+m)(kx2+m)=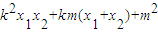 ,
,
①若OM⊥ON,则x1x2+y1y2=0,∴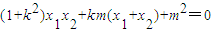 ,
,
∴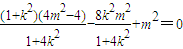 ,化为
,化为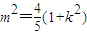 ,此时点O到直线l的距离d=
,此时点O到直线l的距离d=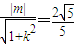 .
.
②∵kBM•kBN=- ,∴
,∴ ,
,
∴x1x2-2(x1+x2)+4+4y1y2=0,
∴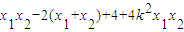 +
+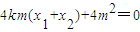 ,
,
代入化为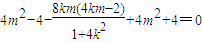 ,化简得m(m+2k)=0,解得m=0或m=-2k.
,化简得m(m+2k)=0,解得m=0或m=-2k.
当m=0时,直线l恒过原点;
当m=-2k时,直线l恒过点(2,0),此时直线l与曲线C最多有一个公共点,不符合题意,
综上可知:直线l恒过定点(0,0).
点评:本题综合考查了直线与椭圆相交问题转化为直线l的方程与椭圆方程联立得到根与系数的关系、OM⊥ON?x1x2+y1y2=0、点到直线的距离公式、斜率计算公式等基础知识与基本能力,考查了推理能力和计算能力.
(2)把直线l的方程与椭圆方程联立得到根与系数的关系,①利用OM⊥ON?x1x2+y1y2=0即可得到k与m的关系,再利用点到直线的距离公式即可证明;
②利用斜率计算公式和根与系数的关系即可得出k与m的关系,进而证明结论.
解答:解:(1)由题意得
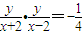 ,(x≠±2),即x2+4y2=4(x≠±2).
,(x≠±2),即x2+4y2=4(x≠±2).∴动点P的轨迹C的方程是
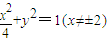 .
.(2)设点M(x1,y1),N(x2,y2),联立
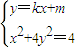 ,化为(1+4k2)x2+8kmx+4m2-4=0,
,化为(1+4k2)x2+8kmx+4m2-4=0,∴△=64k2m2-16(m2-1)(1+4k2)=16(1+4k2-m2)>0.
∴
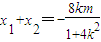 ,
,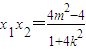 .
.∴y1y2=(kx1+m)(kx2+m)=
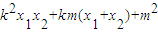 ,
,①若OM⊥ON,则x1x2+y1y2=0,∴
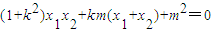 ,
,∴
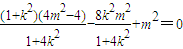 ,化为
,化为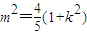 ,此时点O到直线l的距离d=
,此时点O到直线l的距离d=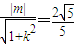 .
.②∵kBM•kBN=-
 ,∴
,∴ ,
,∴x1x2-2(x1+x2)+4+4y1y2=0,
∴
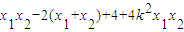 +
+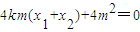 ,
,代入化为
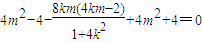 ,化简得m(m+2k)=0,解得m=0或m=-2k.
,化简得m(m+2k)=0,解得m=0或m=-2k.当m=0时,直线l恒过原点;
当m=-2k时,直线l恒过点(2,0),此时直线l与曲线C最多有一个公共点,不符合题意,
综上可知:直线l恒过定点(0,0).
点评:本题综合考查了直线与椭圆相交问题转化为直线l的方程与椭圆方程联立得到根与系数的关系、OM⊥ON?x1x2+y1y2=0、点到直线的距离公式、斜率计算公式等基础知识与基本能力,考查了推理能力和计算能力.

练习册系列答案
相关题目
已知平面上的动点P到定点F(a,0)的距离比到y轴的距离大a(a>0),则动点P的轨迹是( )
| A、抛物线 | B、射线 | C、抛物线或射线 | D、椭圆 |
 .
.