题目内容
设曲线C:f(x)=x3-ax+b(a,b∈R)(1)若函数g(x)=lnx-
 [f′(x)+a]-2x存调递减区间,求a的取值范围;
[f′(x)+a]-2x存调递减区间,求a的取值范围;(2)若过曲线C外的点A(1,0)作曲线C的切线恰有三条,求a,b满足的关系式.
【答案】分析:(1)由已知中f(x)=x3-ax+b(a,b∈R),我们易求出函数的导函数f′(x),进而给出函数g(x)=lnx-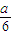 [f′(x)+a]-2x的解析式,若函数g(x)存调递减区间,则g′(x)=
[f′(x)+a]-2x的解析式,若函数g(x)存调递减区间,则g′(x)=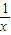 -ax-2<0在(0,+∞)上有解,构造函数h(x)=
-ax-2<0在(0,+∞)上有解,构造函数h(x)=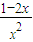 ,求出其最小值,即可得到答案.
,求出其最小值,即可得到答案.
(2)由(1)中导函数f′(x)的解析式,我们设出切点坐标,则可以得到直线的切线方程,由于切线过A点,将A点坐标代入即可得到关于参数的方程,又由已知中过点A(1,0)的曲线C的切线恰有三条,则对应方程恰有三个不同的根,构造函数后,可以转化为函数恰有三个零点,结合三次函数的图象性质,判断出函数的极小值小于0,极大值大于0,构造关于参数的方程组,解方程组,即可得到答案.
解答:解:(1)∵f′(x)=3x2-a,
∴g(x)=lnx-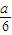 [f′(x)+a]-2x=lnx-
[f′(x)+a]-2x=lnx-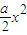 -2x(x>0)
-2x(x>0)
∴g′(x)=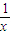 -ax-2
-ax-2
若使g(x) 存在单调减区间,
则g′(x)=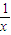 -ax-2<0在(0,+∞)上有解
-ax-2<0在(0,+∞)上有解
即a>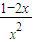 在(0,+∞)上有解
在(0,+∞)上有解
设h(x)=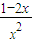 =
=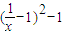
则h(x)的最小值为-1
若a>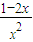 在(0,+∞)上有解
在(0,+∞)上有解
则a>-1
(2)∵f′(x)=3x2-a,
过点A(1,0)作曲线C的切线,设切点坐标为(c,f(c))
则切线方程为 y-(c3-ac+b)=(3c2-a)(x-a)
即y=(3c2-a)x-2c3+b
又∵切线过A(1,0)点
则(3c2-a)-2c3+b=0
即-2c3+3c2-a+b=0
又由过点A(1,0)的曲线C的切线恰有三条,
∴方程-2c3+3c2-a+b=0恰好有三个根,
令h(c)=-2c3+3c2-a+b
则h′(c)=-6c2+6c
则函数h(c)=-2c3+3c2-a+b在c=0时取极小值,在c=1时取极大值,
若方程-2c3+3c2-a+b=0恰好有三个根,
则h(0)=-a+b<0,h(1)=1-a+b>0
即a,b满足的关系式为0<a-b<1
点评:本题考查的知识点是利用民数研究曲线上某点的切线方程,利用导数研究函数的单调性,其中根据函数的解析式,求出导函数的解析式是解答本题的关键.
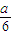 [f′(x)+a]-2x的解析式,若函数g(x)存调递减区间,则g′(x)=
[f′(x)+a]-2x的解析式,若函数g(x)存调递减区间,则g′(x)=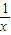 -ax-2<0在(0,+∞)上有解,构造函数h(x)=
-ax-2<0在(0,+∞)上有解,构造函数h(x)=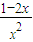 ,求出其最小值,即可得到答案.
,求出其最小值,即可得到答案.(2)由(1)中导函数f′(x)的解析式,我们设出切点坐标,则可以得到直线的切线方程,由于切线过A点,将A点坐标代入即可得到关于参数的方程,又由已知中过点A(1,0)的曲线C的切线恰有三条,则对应方程恰有三个不同的根,构造函数后,可以转化为函数恰有三个零点,结合三次函数的图象性质,判断出函数的极小值小于0,极大值大于0,构造关于参数的方程组,解方程组,即可得到答案.
解答:解:(1)∵f′(x)=3x2-a,
∴g(x)=lnx-
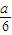 [f′(x)+a]-2x=lnx-
[f′(x)+a]-2x=lnx-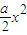 -2x(x>0)
-2x(x>0)∴g′(x)=
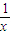 -ax-2
-ax-2若使g(x) 存在单调减区间,
则g′(x)=
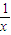 -ax-2<0在(0,+∞)上有解
-ax-2<0在(0,+∞)上有解即a>
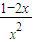 在(0,+∞)上有解
在(0,+∞)上有解设h(x)=
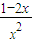 =
=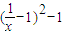
则h(x)的最小值为-1
若a>
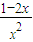 在(0,+∞)上有解
在(0,+∞)上有解则a>-1
(2)∵f′(x)=3x2-a,
过点A(1,0)作曲线C的切线,设切点坐标为(c,f(c))
则切线方程为 y-(c3-ac+b)=(3c2-a)(x-a)
即y=(3c2-a)x-2c3+b
又∵切线过A(1,0)点
则(3c2-a)-2c3+b=0
即-2c3+3c2-a+b=0
又由过点A(1,0)的曲线C的切线恰有三条,
∴方程-2c3+3c2-a+b=0恰好有三个根,
令h(c)=-2c3+3c2-a+b
则h′(c)=-6c2+6c
则函数h(c)=-2c3+3c2-a+b在c=0时取极小值,在c=1时取极大值,
若方程-2c3+3c2-a+b=0恰好有三个根,
则h(0)=-a+b<0,h(1)=1-a+b>0
即a,b满足的关系式为0<a-b<1
点评:本题考查的知识点是利用民数研究曲线上某点的切线方程,利用导数研究函数的单调性,其中根据函数的解析式,求出导函数的解析式是解答本题的关键.

练习册系列答案
相关题目
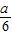 [f′(x)+a]-2x存调递减区间,求a的取值范围;
[f′(x)+a]-2x存调递减区间,求a的取值范围;