题目内容
设曲线C:f(x)=lnx-ex(e=2.71828…),f′(x)表示f(x)导函数.(I)求函数f(x)的极值;
(II)数列{an}满足a1=e,an+1=2f′(
| 1 | an |
分析:(1)先对函数进行求导,讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值点,求出极值即可.
(2)根据递推关系求出数列通项an,假设数列{an}中存在成等差数列的三项ar,as,at,寻求矛盾即可.
(2)根据递推关系求出数列通项an,假设数列{an}中存在成等差数列的三项ar,as,at,寻求矛盾即可.
解答:解:(I)f′(x)=
-e=
=0,得x=
当x变化时,f′(x)与f(x)变化情况如下表:

∴当x=
时,f(x)取得极大值f(
)=-2,没有极小值;
(II)∵an+1=2f′(
)+3e,
∴an+1=2an+e
=2,
∴an=e(2n-1)
假设数列{an}中存在成等差数列的三项ar,as,at(r<s<t),
则2as=ar+at,2e(2s-1)=e(2r-1)+e(2t-1),2s+1=2r+2t,
∴2s-r+1=1+2t-r又s-r+1>0,t-r>0,
∴2s-r+1为偶数,1+2t-r为奇数,假设不成立
因此,数列{an}中不存在成等差数列的三项.
| 1 |
| x |
| 1-ex |
| x |
| 1 |
| e |
当x变化时,f′(x)与f(x)变化情况如下表:

∴当x=
| 1 |
| e |
| 1 |
| e |
(II)∵an+1=2f′(
| 1 |
| an |
∴an+1=2an+e
| an+1+e |
| an+e |
∴an=e(2n-1)
假设数列{an}中存在成等差数列的三项ar,as,at(r<s<t),
则2as=ar+at,2e(2s-1)=e(2r-1)+e(2t-1),2s+1=2r+2t,
∴2s-r+1=1+2t-r又s-r+1>0,t-r>0,
∴2s-r+1为偶数,1+2t-r为奇数,假设不成立
因此,数列{an}中不存在成等差数列的三项.
点评:本题主要考查了利用导数研究函数的极值,以及等差数列的性质,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
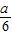 [f′(x)+a]-2x存调递减区间,求a的取值范围;
[f′(x)+a]-2x存调递减区间,求a的取值范围; [f′(x)+a]-2x存调递减区间,求a的取值范围;
[f′(x)+a]-2x存调递减区间,求a的取值范围;