题目内容
已知半径为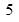 的圆的圆心在
的圆的圆心在 轴上,且与直线
轴上,且与直线 相切.圆心的横坐标是整数。
相切.圆心的横坐标是整数。
(1)求圆的方程;
(2)设直线
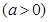 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
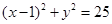 ;(2)(
;(2)(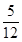 ,+
,+ )(3)
)(3) .
.
【解析】本试题主要考查圆的方程的求解,以及直线与圆的位置关系的运用。
解:(Ⅰ)设圆心为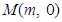 (
(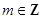 ).由于圆与直线
).由于圆与直线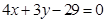 相切,且半径为
相切,且半径为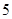 ,所以
,所以
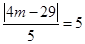 ,即
,即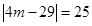 .因为
.因为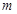 为整数,故
为整数,故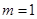 .
.
故所求圆的方程为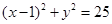 . …………………………………4分
. …………………………………4分
(2)把直线ax-y+5=0,即y=ax+5代入圆的方程,消去y整理,的
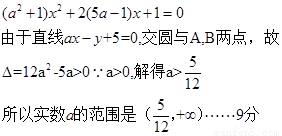
(Ⅲ)设符合条件的实数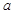 存在,由于,则直线
存在,由于,则直线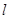 的斜率为
的斜率为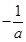
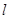 的方程为
的方程为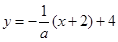 ,即
,即
由于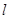 垂直平分弦AB,故圆心
垂直平分弦AB,故圆心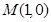 必在
必在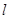 上,
上,
所以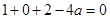 ,解得
,解得 。由于
。由于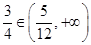 ,故存在实数
,故存在实数
使得过点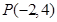 的直线
的直线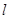 垂直平分弦AB………………………14分
垂直平分弦AB………………………14分

练习册系列答案
相关题目
 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切. 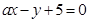
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.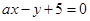
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.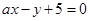
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;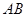 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的圆的圆心在
的圆的圆心在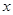 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数