题目内容
已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线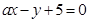
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
解:(1)设圆心为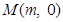 (
(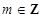 ).由于圆与直线
).由于圆与直线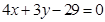 相切,且半径为
相切,且半径为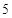 ,所以
,所以
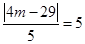 ,即
,即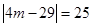 .因为
.因为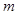 为整数,故
为整数,故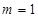 .
.
故所求圆的方程为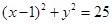 .
…………………………………4分
.
…………………………………4分
(Ⅱ)把直线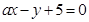 即
即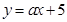 .代入圆的方程,消去
.代入圆的方程,消去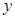 整理,得
整理,得
 .
.
由于直线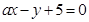 交圆于
交圆于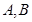 两点,故
两点,故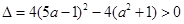 .
.
即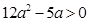 ,由于
,由于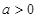 ,解得
,解得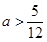 .
.
所以实数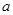 的取值范围是
的取值范围是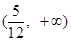 .………………………………………8分
.………………………………………8分
(3)设符合条件的实数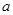 存在,由于
存在,由于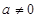 ,则直线
,则直线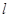 的斜率为
的斜率为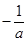 ,
,
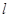 的方程为
的方程为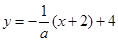 ,
即
,
即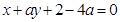 .
.
由于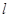 垂直平分弦
垂直平分弦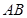 ,故圆心
,故圆心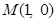 必在
必在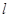 上.
上.
所以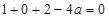 ,解得
,解得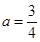 .由于
.由于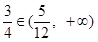 ,
,
故存在实数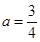 ,使得过点
,使得过点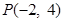 的直线
的直线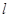 垂直平分弦
垂直平分弦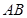 .……………12分
.……………12分
【解析】此题考查了直线与圆相交的性质,以及直线与圆的位置关系,涉及的知识有:点到直线的距离公式,一元二次方程根的判别式与解的关系,一元二次不等式的解法,解题的关键是:当直线与圆相切时,圆心到直线的距离等于圆的半径;将直线与圆的方程联立消去y后,得到关于x的一元二次方程,此一元二次方程的解的个数决定了直线与圆交点的个数(1)设圆心M的坐标为(m,0),且m是整数,由圆C与已知直线垂直,得到圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解得到m的值,进而确定出圆C的方程;
(2)由直线ax-y+5=0,表示出y,代入圆的方程消去y,得到关于x的一元二次方程,根据直线与圆有两个交点,得到根的判别式大于0,列出关于a的不等式,求出不等式的解集即可得到a的取值范围.
(3)假设存在利用推理得到结论。

练习册系列答案
相关题目
 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.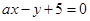
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数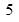 的圆的圆心在
的圆的圆心在 轴上,且与直线
轴上,且与直线 相切.圆心的横坐标是整数。
相切.圆心的横坐标是整数。
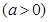 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.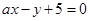
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;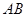 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的圆的圆心在
的圆的圆心在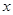 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数