题目内容
在“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
(1)补全下列频率分布直方图;

(2)估计这次“家电下乡”活动中,该品牌用户满意度超过6的概率;
(3)估算这20名用户满意度的中位数(写出计算过程);
(4)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |

(2)估计这次“家电下乡”活动中,该品牌用户满意度超过6的概率;
(3)估算这20名用户满意度的中位数(写出计算过程);
(4)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
分析:(1)频率分布直方图如图.
(2)样本中,该品牌用户满意度超过6的有5+8=13个,样本容量为20,由此可得该品牌用户满意度
超过6的概率.
(3)频率分布直方图中,结合中位数的定义可得中位数在[6,8)内,设为x.根据 0.05+0.1+0.20+0.125(x-6)=0.5,可得x的值.
(4)所有的取法有
=10种,满足|x-y|<1的取法共有7个(从总数中除去(6.5,7.5)、(6.5,7.5)、(6.5,7.9)这3个),可得|x-y|<1的概率.
(2)样本中,该品牌用户满意度超过6的有5+8=13个,样本容量为20,由此可得该品牌用户满意度
超过6的概率.
(3)频率分布直方图中,结合中位数的定义可得中位数在[6,8)内,设为x.根据 0.05+0.1+0.20+0.125(x-6)=0.5,可得x的值.
(4)所有的取法有
| C | 2 5 |
解答:解:(1)频率分布直方图如图: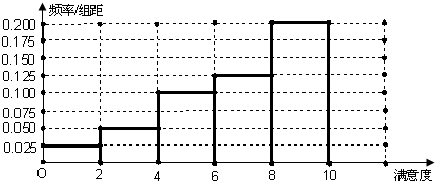 .
.
(2)样本中,该品牌用户满意度超过6的有5+8=13个,样本容量为20,
故该品牌用户满意度超过6的概率为
.
(3)频率分布直方图中,从左到右每一组的频率分别为0.05、0.10、0.20、0.25、0.40,
由于0.05+0.1+0.20=0.35<0.5,而0.05+0.1+0.20+0.25=0.60>0.5,
故中位数在[6,8)内,设为x.根据 0.05+0.1+0.20+0.125(x-6)=0.5,可得x=7.2,
即中位数为0.72.
(4)所有的取法有
=10种,满足|x-y|<1的取法共有7个(从总数中除去(6.5,7.5)、
(6.5,7.5)、(6.5,7.9)这3个),
故|x-y|<1的概率为
.
 .
.(2)样本中,该品牌用户满意度超过6的有5+8=13个,样本容量为20,
故该品牌用户满意度超过6的概率为
| 13 |
| 20 |
(3)频率分布直方图中,从左到右每一组的频率分别为0.05、0.10、0.20、0.25、0.40,
由于0.05+0.1+0.20=0.35<0.5,而0.05+0.1+0.20+0.25=0.60>0.5,
故中位数在[6,8)内,设为x.根据 0.05+0.1+0.20+0.125(x-6)=0.5,可得x=7.2,
即中位数为0.72.
(4)所有的取法有
| C | 2 5 |
(6.5,7.5)、(6.5,7.9)这3个),
故|x-y|<1的概率为
| 7 |
| 10 |
点评:本题考查古典概型及其概率计算公式的应用,频率分布直方图,属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目