题目内容
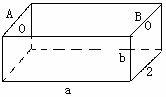
为处理含有某种杂质的污水，要制造一底宽为2 m的无盖长方体沉淀箱.污水从A孔流入，经沉淀后从B孔流出.设箱体的长度为 a m，高度为b m，如图所示.已知流出的水中含杂质的质量分数与a、b的乘积ab成反比.现有制箱材料60 m2，问：当a，b各为多少时，经沉淀后流出的水中该杂质的质量分数最小？（A、B两孔的面积忽略不计）思路解析：用a、b表示流出的水中杂质的质量分数，找到a、b的关系，建立数学模型求最值. 解法一：设y为流出的水中杂质的质量分数，则y= 根据题设有4b+2ab+2a=60(a＞0,b＞0),得b= 于是y= = = 当a+2= 将a=6代入①式，得b=3. 故当a为6 m，b为3 m时，经沉淀后流出的水中该杂质的质量分数最小. 解法二：依题意，当ab最大时，流出的水中该杂质的质量分数最小. 由题设知4b+2ab+2a=60(a＞0,b＞0),即a+2b+ab=30(a＞0,b＞0). ∵a+2b≥2· ∴2 当且仅当a=2b时，上式取等号. 设 ∵ab=t2,∴0＜ab≤18, 即当a=2b时，ab取得最大值，其最大值为18. ∴2b2=18. 解得b=3,a=6. 故当a为6 m，b为3 m时，经沉淀后流出的水中该杂质的质量分数最小. 评注：解法一观察到题目有“已知流出的水中含杂质的质量分数与a、b的乘积ab成反比”，这样建立函数关系y= 解法二是考虑到“已知流出的水中含杂质的质量分数与ab成反比”.那么要求流出水中杂质的质量分数最小，只需求ab的最大值即可.解法二是最优解法.
,其中k＞0，为比例系数.依题意，即所求的a，b值使y值最小.
(0＜a＜30). ①
=
=
≥
.
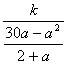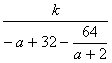
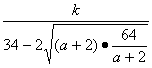
时，取等号，y达到最小值,这时a=6，a=-10（舍去）.
,
+ab≤30,
=t(t＞0),则ab=t2.∴t2+2
t-30≤0.解得0＜t≤3
.
(k＞0)，再利用箱体材料60 m2的限制得出4b+2ab+2a=60，这时，在条件4b+2ab+2a=60下，求y的最小值.
新锐图书复习计划期末寒假衔接系列答案
高考导航系列丛书假期作业寒假系列答案
寒假作业教育科学出版社系列答案
寒假假期快乐练南方出版社系列答案
寒假学习乐园南方出版社系列答案
康华传媒考出好成绩中考试题汇编系列答案
寒假作业甘肃教育出版社系列答案
中考211系列答案
寒假生活四川大学出版社系列答案
响叮当寒假作业广州出版社系列答案
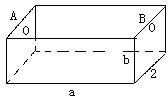如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出．设箱体的长度为a米，高度为b米．已知流出的水中该杂质的质量分数与a，b的乘积ab成反比．现有制箱材料60平方米．问当a，b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A、B孔的面积忽略不计）．
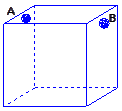为处理含有某种杂质的污水，要制造一个底宽为2米的无盖长方体沉淀箱（如图），污水从A孔流入，经沉淀后从B孔流出，设箱体的长度为a米，高度为b米，已知流出的水中该杂质的质量分数与a、b的乘积ab成反比，现有制箱材料60平方米，问当a、b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A、B孔的面积忽略不计）？
孔流入，经沉淀后从
孔流出，设箱体的长为
米，高为
米．已知流出的水中该杂质的质量分数与
成反比，现有制箱材料60平方米，问当
