��Ŀ����
��֪��Բ����Ϊ ���������˵�ΪA��B�������϶˵�ΪC��
���������˵�ΪA��B�������϶˵�ΪC��
��1������Բ��������Ϊ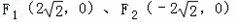 ����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
��2�����ڣ�1���е���Բ���̣�����CΪֱ�Ƕ�����ڽ�����Բ�ĵ���ֱ��������CDE����ֱ��CE��б��Ϊk��k��0��������k����Ĺ�ϵ��ʽ��
��3����C����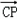 ��ֱ��
��ֱ��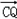 ����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
 ���������˵�ΪA��B�������϶˵�ΪC��
���������˵�ΪA��B�������϶˵�ΪC����1������Բ��������Ϊ
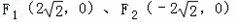 ����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣���2�����ڣ�1���е���Բ���̣�����CΪֱ�Ƕ�����ڽ�����Բ�ĵ���ֱ��������CDE����ֱ��CE��б��Ϊk��k��0��������k����Ĺ�ϵ��ʽ��
��3����C����
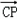 ��ֱ��
��ֱ��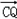 ����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ��⣺��1������֪��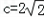 ��
�� ��
��
������������ã�a=3��b=1��
������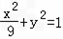
��2����������CE���ڵ�ֱ�߷���Ϊy=kx+1��k��0����
������Բ���̲������ã���1+9k2��x2+18kx=0���� ��
��
ͬ��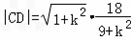
��|CE|=|CD|��k3+9k2+9k+1=0������k+1����k2+8k+1��=0
��3��������ã�T��0����b������֪ ��
��
��P��x1��y1����Q��x2��y2��

x1x2=����y1��b����y2��b��
���� ��
�� ��
��
ͬ��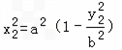 ��
��
���� ��
��
�Ӷ���
����
�� ��Ϊ��ֵ����
��Ϊ��ֵ����
�Ա���ʽ��֪��ѡȡT��0����b�������ֱ��TP��б����TQ��б��֮��Ϊ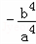
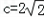 ��
�� ��
��������������ã�a=3��b=1��
������
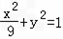
��2����������CE���ڵ�ֱ�߷���Ϊy=kx+1��k��0����
������Բ���̲������ã���1+9k2��x2+18kx=0����
 ��
��ͬ��
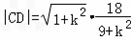
��|CE|=|CD|��k3+9k2+9k+1=0������k+1����k2+8k+1��=0
��3��������ã�T��0����b������֪
 ��
����P��x1��y1����Q��x2��y2��

x1x2=����y1��b����y2��b��
����
 ��
�� ��
��ͬ��
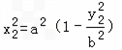 ��
������
 ��
���Ӷ���

����

��
 ��Ϊ��ֵ����
��Ϊ��ֵ�����Ա���ʽ��֪��ѡȡT��0����b�������ֱ��TP��б����TQ��б��֮��Ϊ
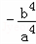

��ϰ��ϵ�д�
�����Ŀ
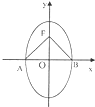 ��ͼ��ʾ����֪��Բ����Ϊ
��ͼ��ʾ����֪��Բ����Ϊ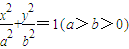 ���������˵�ΪA��B�������϶˵�ΪC��
���������˵�ΪA��B�������϶˵�ΪC��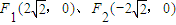 ����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�
����M����Բ���˶�������ABM��������Ϊ3ʱ��������Բ���̣�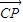 ��ֱ��
��ֱ��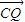 ����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�
����P��Q����Բ�ϣ�������y�����Ƿ����һ��Tʹ��ֱ��TP��б����TQ��б��֮��Ϊ��ֵ��������ڣ��ҳ���T������Ͷ�ֵ����������ڣ�˵�����ɣ�