题目内容
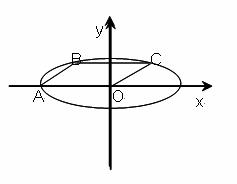
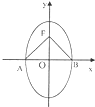 如图所示:已知椭圆方程为
如图所示:已知椭圆方程为| y2 |
| a2 |
| x2 |
| b2 |
(1)求椭圆离心率;
(2)若椭圆的短轴长为2,过F的直线与椭圆相交的弦长为
| 3 |
| 2 |
| 2 |
分析:(1)根据△ABF为直角三角形,可得2|OF|=|AB|,从而可得c=b,即c2=a2-c2,从而可得椭圆的离心率;
(2)求出椭圆方程,设过F的直线方程为y=kx+1,代入椭圆方程,利用韦达定理,计算弦长,即可求得直线的方程.
(2)求出椭圆方程,设过F的直线方程为y=kx+1,代入椭圆方程,利用韦达定理,计算弦长,即可求得直线的方程.
解答:解:(1)由题意,∵△ABF为直角三角形,∴2|OF|=|AB|,则
∵A,B是椭圆与短轴的两个交点,F是椭圆的焦点,
∴c=b,∴c2=a2-c2,
∴a2=2c2,
∴e=
=
(2)由题意,F(0,1),b=1,c=1,∴a2=2,
∴椭圆方程为
+x2=1
设过F的直线方程为y=kx+1,代入椭圆方程,消元可得(k2+2)x2+2kx-1=0
设交点坐标分别为(x1,y1),(x2,y2),则x1+x2=-
,x1x2=-
∴过F的直线与椭圆相交的弦长为
|x1-x2|=
×
=
×
=
∵过F的直线与椭圆相交的弦长为
,
∴
=
∴k=±
∴弦所在直线的方程为y=±
x+1
∵A,B是椭圆与短轴的两个交点,F是椭圆的焦点,
∴c=b,∴c2=a2-c2,
∴a2=2c2,
∴e=
| c |
| a |
| ||
| 2 |
(2)由题意,F(0,1),b=1,c=1,∴a2=2,
∴椭圆方程为
| y2 |
| 2 |
设过F的直线方程为y=kx+1,代入椭圆方程,消元可得(k2+2)x2+2kx-1=0
设交点坐标分别为(x1,y1),(x2,y2),则x1+x2=-
| 2k |
| k2+2 |
| 1 |
| k2+2 |
∴过F的直线与椭圆相交的弦长为
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(-
|
2
| ||
| k2+2 |
∵过F的直线与椭圆相交的弦长为
| 3 |
| 2 |
| 2 |
∴
2
| ||
| k2+2 |
| 3 |
| 2 |
| 2 |
∴k=±
| 2 |
∴弦所在直线的方程为y=±
| 2 |
点评:本题考查椭圆的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,联立方程,利用韦达定理解题是关键.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
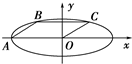 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 如图所示,已知椭圆C:
如图所示,已知椭圆C: