题目内容
设函数f（x）=
cos2ωx+sinωxcosωx+a（其中ω＞0，a∈R），且f（x）的图象在y轴右侧的第一个最高点的横坐标为
．
（1）求ω的值；
（2）如果f（x）在区间[-
，
]上的最小值为
，求a的值；
（3）证明：直线5x-2y+c=0与函数y=f（x）的图象不相切．
| 3 |
| π |
| 12 |
（1）求ω的值；
（2）如果f（x）在区间[-
| π |
| 6 |
| 5π |
| 12 |
| 3 |
（3）证明：直线5x-2y+c=0与函数y=f（x）的图象不相切．
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：函数的性质及应用
分析：（1）化简三角函数式，求出周期，利用周期公式求ω；
（2）利用（1）的解析式求2x+
的范围；
（3）对f（x）求导，得到曲线切线范围，与直线斜率比较，得到答案．
（2）利用（1）的解析式求2x+
| π |
| 3 |
（3）对f（x）求导，得到曲线切线范围，与直线斜率比较，得到答案．
解答：
解：（1）f（x）=
×
+
sin2ωx+a=
sin2ωx+
cos2ωx+
+a=sin（2ωx+
）+
+a，由题意，2ω×
+
=
，所以ω=1；
（2）由（1）知，f（x）=sin（2x+
）+
+a，
∵x∈[-
，
]，∴2x+
∈[0，
]，
∴-
≤sin（2x+
）≤1，
∴f（x）在区间[-
，
]上的最小值为-
+
+a=
，解得a=
；
（3）∵f′（x）=2cos（2x+
）
∴|f′（x）|≤2，∴曲线y=f（x）的切线斜率的取值范围是[-2，2]，
而直线的切线斜率=
＞2，
∴直线5x-2y+c=0与函数y=f（x）的图象不相切．…（12分）
| 3 |
| 1+cos2ωx |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
（2）由（1）知，f（x）=sin（2x+
| π |
| 3 |
| ||
| 2 |
∵x∈[-
| π |
| 6 |
| 5π |
| 12 |
| π |
| 3 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 3 |
∴f（x）在区间[-
| π |
| 6 |
| 5π |
| 12 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
1+
| ||
| 2 |
（3）∵f′（x）=2cos（2x+
| π |
| 3 |
∴|f′（x）|≤2，∴曲线y=f（x）的切线斜率的取值范围是[-2，2]，
而直线的切线斜率=
| 5 |
| 2 |
∴直线5x-2y+c=0与函数y=f（x）的图象不相切．…（12分）
点评：本题考查了三角函数解析式的化简以及最值求法，关键是正确利用倍角公式等化简三角函数式，属于中档题．
练习册系列答案
高中必刷题系列答案
相关题目
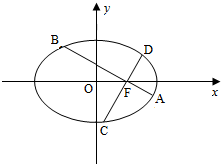如图，在平面直角坐标系xOy中，椭圆