题目内容
设 都是{x|0≤x≤1}的子集,如果b-a叫做集合{x|a≤x≤b}的长度,则集合M∩N的长度的最小值是
都是{x|0≤x≤1}的子集,如果b-a叫做集合{x|a≤x≤b}的长度,则集合M∩N的长度的最小值是
- A.

- B.

- C.

- D.

D
分析:由m≥0,且m+ ≤1,求出m∈[0,
≤1,求出m∈[0, ],由n-
],由n- ≥0,且n≤1,求出n∈[
≥0,且n≤1,求出n∈[ ,1].所以M={x|0≤x≤
,1].所以M={x|0≤x≤ },N={x|
},N={x| ≤x≤1},或M={x|
≤x≤1},或M={x| ≤x≤1},N={x|0≤x≤
≤x≤1},N={x|0≤x≤ },所以M∩N={x|
},所以M∩N={x| ≤x≤
≤x≤ },或{x|
},或{x| ≤x≤
≤x≤ }.
}.
由此能求出集合M∩N的长度的最小值.
解答:由m≥0,且m+ ≤1,求出m∈[0,
≤1,求出m∈[0, ],
],
由n- ≥0,且n≤1,求出n∈[
≥0,且n≤1,求出n∈[ ,1],
,1],
分别把m,n的两端值代入求出:
M={x|0≤x≤ },N={x|
},N={x| ≤x≤1},
≤x≤1},
或M={x| ≤x≤1},N={x|0≤x≤
≤x≤1},N={x|0≤x≤ },
},
所以M∩N={x| ≤x≤
≤x≤ },
},
或{x| ≤x≤
≤x≤ }.
}.
所以b-a=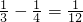 ,或
,或 ,
,
综上所述,集合M∩N的长度的最小值是 .
.
故选D.
点评:本题考查集合的交运算的应用,解题时要认真审题,注意正确理解集合{x|a≤x≤b}的长度的概念.
分析:由m≥0,且m+
 ≤1,求出m∈[0,
≤1,求出m∈[0, ],由n-
],由n- ≥0,且n≤1,求出n∈[
≥0,且n≤1,求出n∈[ ,1].所以M={x|0≤x≤
,1].所以M={x|0≤x≤ },N={x|
},N={x| ≤x≤1},或M={x|
≤x≤1},或M={x| ≤x≤1},N={x|0≤x≤
≤x≤1},N={x|0≤x≤ },所以M∩N={x|
},所以M∩N={x| ≤x≤
≤x≤ },或{x|
},或{x| ≤x≤
≤x≤ }.
}.由此能求出集合M∩N的长度的最小值.
解答:由m≥0,且m+
 ≤1,求出m∈[0,
≤1,求出m∈[0, ],
],由n-
 ≥0,且n≤1,求出n∈[
≥0,且n≤1,求出n∈[ ,1],
,1],分别把m,n的两端值代入求出:
M={x|0≤x≤
 },N={x|
},N={x| ≤x≤1},
≤x≤1},或M={x|
 ≤x≤1},N={x|0≤x≤
≤x≤1},N={x|0≤x≤ },
},所以M∩N={x|
 ≤x≤
≤x≤ },
},或{x|
 ≤x≤
≤x≤ }.
}.所以b-a=
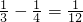 ,或
,或 ,
,综上所述,集合M∩N的长度的最小值是
 .
.故选D.
点评:本题考查集合的交运算的应用,解题时要认真审题,注意正确理解集合{x|a≤x≤b}的长度的概念.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
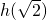 ;
;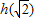 ;
;