题目内容
已知动圆过定点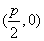 ,且与直线
,且与直线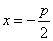 相切,其中
相切,其中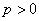
(1)求动圆圆心的轨迹方程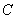 ;
;
(2)设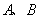 是轨迹
是轨迹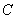 上异于原点
上异于原点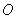 的两个不同点,直线
的两个不同点,直线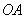 和
和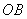 的倾斜角分别为
的倾斜角分别为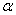 和
和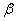 ,当
,当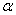 ,
,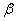 变化且
变化且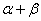 为定值
为定值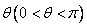 时,直线
时,直线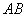 恒过定点,并求出该点的坐标.
恒过定点,并求出该点的坐标.
【答案】
解:(I)如图,设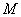 为动圆圆心,
为动圆圆心,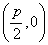 为记为
为记为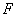 ,过点
,过点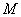 作直线
作直线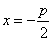 的垂线,垂足为
的垂线,垂足为 ,由题意知:
,由题意知: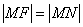 即动点
即动点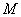 到定点
到定点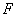 与定直线
与定直线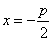 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点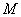 的轨迹为抛物线,其中
的轨迹为抛物线,其中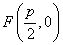 为焦点,
为焦点,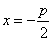 为准线,所以轨迹方程为
为准线,所以轨迹方程为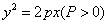 ;
4分
;
4分
(II)如图,设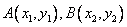 ,由题意得
,由题意得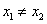 (否则
(否则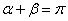 )且
)且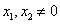 所以直线
所以直线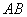 的斜率存在,设其方程为
的斜率存在,设其方程为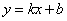 ,显然
,显然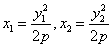 ,将
,将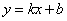 与
与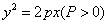 联立消去
联立消去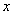 ,得
,得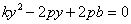 由韦达定理知
由韦达定理知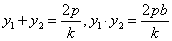 ①
①
(1)当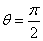 时,即
时,即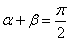 时,
时,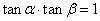 所以
所以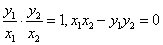 ,
,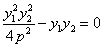 所以
所以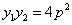 由①知:
由①知: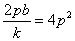 所以
所以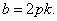 因此直线
因此直线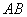 的方程可表示为
的方程可表示为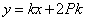 ,即
,即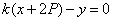 所以直线
所以直线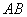 恒过定点
恒过定点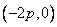 8分
8分
(2)当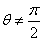 时,由
时,由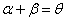 ,得
,得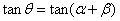 =
=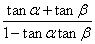 =
=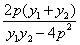
将①式代入上式整理化简可得: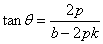 ,所以
,所以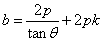 ,此时,直线
,此时,直线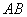 的方程可表示为
的方程可表示为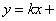
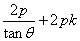 即
即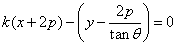
所以直线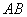 恒过定点
恒过定点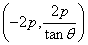
所以由(1)(2)知,当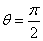 时,直线
时,直线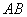 恒过定点
恒过定点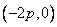 ,当
,当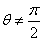 时直线
时直线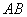 恒过定点
恒过定点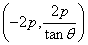 .
13分
.
13分

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 (1) 求动圆的圆心轨迹
(1) 求动圆的圆心轨迹 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点是
的对称轴为坐标轴,一个焦点是 ,点
,点 在椭圆
在椭圆 的方程及其椭圆
的方程及其椭圆 与轨迹
与轨迹 处的切线平行,且直线
处的切线平行,且直线 两点,问:是否存在着这样的直线
两点,问:是否存在着这样的直线 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线