题目内容
若有穷数列{an}满足:(1)首项a1=1,末项am=k;(2)an+1=an+1或an+1=2an,(n=1,2,…,m-1),则称数列{an}为k的m阶数列.
(Ⅰ)请写出一个10的6阶数列;
(Ⅱ)设数列{bn}是各项为自然数的递增数列,若k=2b1+2b2+2b3+…2bl(l∈N),且l≥2,求m的最小值.
(Ⅰ)请写出一个10的6阶数列;
(Ⅱ)设数列{bn}是各项为自然数的递增数列,若k=2b1+2b2+2b3+…2bl(l∈N),且l≥2,求m的最小值.
分析:(Ⅰ)根据数列{an}为k的m阶数列的定义可得一个10的6阶数列为:1,2,3,4,5,10或1,2,4,8,9,10.
(Ⅱ)由已知在数列{an}中 an+1=an+1或an+1=2an,当an为偶数时,只需 an-1=
(an≥2).当am为奇数时,必然有 an-1=an-1,(an≥2),an-1是偶数,可继续重复上面的操作.
所以要使项数m最小,只需遇到偶数除以2,遇到奇数则减1.由此可得 m=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bl-bl-1)+(l-1)+1=bl+l.
(Ⅱ)由已知在数列{an}中 an+1=an+1或an+1=2an,当an为偶数时,只需 an-1=
| an |
| 2 |
所以要使项数m最小,只需遇到偶数除以2,遇到奇数则减1.由此可得 m=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bl-bl-1)+(l-1)+1=bl+l.
解答:解:(Ⅰ)1,2,3,4,5,10或1,2,4,8,9,10. …(2分)
(Ⅱ)由已知在数列{an}中 an+1=an+1或an+1=2an,
当an为偶数时,an-1=
(an≥2),或 an-1=an-1.
因为
≤an-1 (an≥2),所以在数列{an}中 1≤ai≤
中i的个数不多于 1≤aj≤an-1 中j的个数,
当要使项数m最小,只需 an-1=
(an≥2). …(5分)
当am为奇数时,必然有 an-1=an-1,(an≥2),an-1是偶数,可继续重复上面的操作.
所以要使项数m最小,只需遇到偶数除以2,遇到奇数则减1.
因为an=k=2b1+2b2+2b3+…2bl(l∈N),且 0≤b1<b2<b3<…<bl,
只需除以2b1,得到 1+2b2-b1+2b3-b1+…+2bl-b1 为奇数;
减1,得到 2b2-b1+2b3-b1+…+2bl-b1 为偶数,
再除以 2b2-b1,得到 1+2b3-b2+2b4-b2+…+2bl-b2 为奇数;
再减1,得到 2b3-b2+2b4-b2+…+2bl-b2 为偶数,
…
最后得到 2bl-bl-1为偶数,除以2bl-bl-1,得到1,即为a1.
所以 m=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bl-bl-1)+(l-1)+1=bl+l. …(13分)
(Ⅱ)由已知在数列{an}中 an+1=an+1或an+1=2an,
当an为偶数时,an-1=
| an |
| 2 |
因为
| an |
| 2 |
| an |
| 2 |
当要使项数m最小,只需 an-1=
| an |
| 2 |
当am为奇数时,必然有 an-1=an-1,(an≥2),an-1是偶数,可继续重复上面的操作.
所以要使项数m最小,只需遇到偶数除以2,遇到奇数则减1.
因为an=k=2b1+2b2+2b3+…2bl(l∈N),且 0≤b1<b2<b3<…<bl,
只需除以2b1,得到 1+2b2-b1+2b3-b1+…+2bl-b1 为奇数;
减1,得到 2b2-b1+2b3-b1+…+2bl-b1 为偶数,
再除以 2b2-b1,得到 1+2b3-b2+2b4-b2+…+2bl-b2 为奇数;
再减1,得到 2b3-b2+2b4-b2+…+2bl-b2 为偶数,
…
最后得到 2bl-bl-1为偶数,除以2bl-bl-1,得到1,即为a1.
所以 m=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bl-bl-1)+(l-1)+1=bl+l. …(13分)
点评:本题主要考查数列的函数特性,k的m阶数列的定义,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
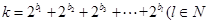 ,且
,且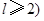 ,求m的最小值.
,求m的最小值.