题目内容
二面角α-l-β的平面角为120°，在面α内，AB⊥l于B，AB=2在平面β内，CD⊥l于D，CD=3，BD=1，M是棱l上的一个动点，则AM+CM的最小值为分析：要求出AM+CM的最小值，可将空间问题转化成平面问题，将二面角展开成平面中在BD上找一点使AM+CM即可，而当A、M、C在一条直线时AM+CM的最小值，从而求出对角线的长即可．
解答：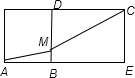
解：将二面角α-l-β平摊开来，即为图形
当A、M、C在一条直线时AM+CM的最小值，最小值即为对角线AC
而AE=5，EC=1
故AC=
故答案为：
解：将二面角α-l-β平摊开来，即为图形当A、M、C在一条直线时AM+CM的最小值，最小值即为对角线AC
而AE=5，EC=1
故AC=
| 26 |
故答案为：
| 26 |
点评：本题主要考查了平面的翻折问题，同时考查了将空间问题转化成平面问题的能力，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
β，BD
