题目内容
5. 如图,y=f(x)是可导函数,直线L:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g′(x)是g(x)的导函数,则g′(3)=( )
如图,y=f(x)是可导函数,直线L:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g′(x)是g(x)的导函数,则g′(3)=( )| A. | -1 | B. | 0 | C. | 2 | D. | 4 |
分析 先从图中求出切线过的点,再求出直线L的方程,利用导数在切点处的导数值为切线的斜率,最后结合导数的概念求出g′(3)的值.
解答 解:∵直线L:y=kx+2是曲线y=f(x)在x=3处的切线,
∴f(3)=1,
又点(3,1)在直线L上,
∴3k+2=1,从而k=$-\frac{1}{3}$,
∴f′(3)=k=$-\frac{1}{3}$,
∵g(x)=xf(x),
∴g′(x)=f(x)+xf′(x)
则g′(3)=f(3)+3f′(3)
=1+3×($-\frac{1}{3}$)
=0,
故选:B.
点评 本题考查导数的几何意义,曲线在切点处的导数值为曲线的切线的斜率.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
17.下列说法正确的是( )
| A. | “x<0”是“ln(x+1)<0”的充要条件 | |
| B. | “?x≥2,x2-3x+2≥0”的否定是“?x<2,x2-3x+2<0” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8 |
16.已知程序框图如图所示,则该程序框图的功能是( )
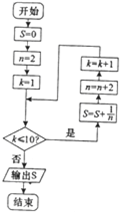

| A. | 求1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$的值 | B. | 求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$…+$\frac{1}{20}$的值 | ||
| C. | 求1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$的值 | D. | 求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$…+$\frac{1}{22}$的值 |
13.已知数列|an|,则an,an+1,an+2(n∈N+)成等比数列是“an+12=anan+2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.阅读如图的程序框图,若输出的y=$\frac{1}{2}$,则输入的x的值可能为( )


| A. | -1 | B. | 0 | C. | 1 | D. | 5 |