题目内容
若点A（a，0），B（0，b），C（1，-1）（a＞0，b＜0）三点共线，则a-b的最小值等于（ ）A．4
B．2
C．1
D．0
【答案】分析：由A、B、C三点共线，可得 kAB=kAC，可得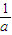 
-
=1，化简 a-b=（a-b）（
-
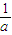）=2-
-
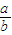，再利用基本不等式可求a-b的最小值．
解答：解析：∵A、B、C三点共线，
∴kAB=kAC，即
=
，∴
-
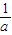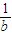=1，
∴a-b=（a-b）（
-
）=2-
-
=2+[（-
）+（-
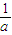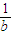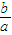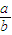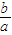）]≥2+2=4（当a=-b=2时取等号），
故选 A．
点评：本题考查直线的斜率公式，基本不等式的应用．
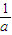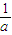-=1，化简 a-b=（a-b）（-）=2--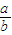，再利用基本不等式可求a-b的最小值．解答：解析：∵A、B、C三点共线，
∴kAB=kAC，即
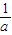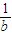=，∴-=1，∴a-b=（a-b）（
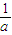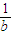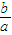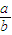-）=2--=2+[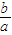（-）+（-）]≥2+2=4（当a=-b=2时取等号），故选 A．
点评：本题考查直线的斜率公式，基本不等式的应用．
练习册系列答案
阅读快车系列答案
相关题目
设直线l：x+y=0，若点A（a，0），B（-2b，4ab）（a＞0，b＞0）满足条件AB∥l，则
的最小值为（ ）
| a+b |
A、1+
| ||||
B、3+2
| ||||
C、
| ||||
D、
|
若点A（a，0），B（0，b），C（1，-1）（a＞0，b＜0）三点共线，则a-b的最小值等于（ ）
| A、4 | B、2 | C、1 | D、0 |