题目内容
设集合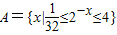 ,B={x|x2-3mx+2m2-m-1<0}.
,B={x|x2-3mx+2m2-m-1<0}.(1)当x∈Z时,求A的非空真子集的个数.
(2)若B=φ,求m的取值范围.
(3)若A?B,求m的取值范围.
【答案】分析:(1)由条件:“x∈Z”知集合A中的元素是整数,进而求它的子集的个数;
(2)由条件:“B=φ”知集合B中的没有任何元素是,得不等式的解集是空集,进而求m;
(3)由条件:“A?B”知集合B是A的子集,结合端点的不等关系列出不等式后解之即得.
解答:解:化简集合A={x|-2≤x≤5},集合B可写为B={x|(x-m+1)(x-2m-1)<0}
(1)∵x∈Z,∴A={-2,-1,0,1,2,3,4,5},即A中含有8个元素,∴A的非空真子集数为28-2=254(个).
(2)显然只有当m-1=2m+1即m=-2时,B=φ.
(3)当B=φ即m=-2时,B=φ⊆A;
当B≠φ即m≠-2时,
(ⅰ)当m<-2时,B=(2m+1,m-1),要B⊆A,只要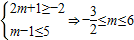 ,所以m的值不存在;
,所以m的值不存在;
(ⅱ)当m>-2时,B=(m-1,2m+1),要B⊆A,只要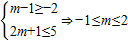 .
.
点评:本题考查集合的子集、集合的包含关系判断及应用以及空集的性质及运算.是一道中档题.
(2)由条件:“B=φ”知集合B中的没有任何元素是,得不等式的解集是空集,进而求m;
(3)由条件:“A?B”知集合B是A的子集,结合端点的不等关系列出不等式后解之即得.
解答:解:化简集合A={x|-2≤x≤5},集合B可写为B={x|(x-m+1)(x-2m-1)<0}
(1)∵x∈Z,∴A={-2,-1,0,1,2,3,4,5},即A中含有8个元素,∴A的非空真子集数为28-2=254(个).
(2)显然只有当m-1=2m+1即m=-2时,B=φ.
(3)当B=φ即m=-2时,B=φ⊆A;
当B≠φ即m≠-2时,
(ⅰ)当m<-2时,B=(2m+1,m-1),要B⊆A,只要
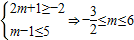 ,所以m的值不存在;
,所以m的值不存在;(ⅱ)当m>-2时,B=(m-1,2m+1),要B⊆A,只要
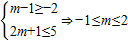 .
.点评:本题考查集合的子集、集合的包含关系判断及应用以及空集的性质及运算.是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合P={x|x<1},集合Q={x|
<0},则P∩Q=( )
| 1 |
| x |
| A、{x|x<0} |
| B、{x|x>1} |
| C、{x|x<0或x>1} |
| D、∅ |
设集合
 ,B={x|x>1},则A∩B等于
,B={x|x>1},则A∩B等于
[
]|
A .{x|x>1} |
B .{x|x>0} |
|
C .{x|x<-1} |
D .{x|x<-1,或x>1} |
 ,B={x|x>1},则A∩B等于
,B={x|x>1},则A∩B等于 ,B={x|x(x-1)<0},则集合A∪B= .
,B={x|x(x-1)<0},则集合A∪B= .