题目内容
设集合M是满足下列条件的函数f(x)的集合:①f(x)的定义域为R;②存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减.
(I)设f1(x)=x•|x-2|,f2(x)=x3-3x2+3x,判断f1(x),f2(x)是否在集合M中,并说明理由;
(II)求证:对任意的实数t,f(x)=
都在集合M中;
(Ⅲ)是否存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,并且有相同的单调区间?请说明理由.
(I)设f1(x)=x•|x-2|,f2(x)=x3-3x2+3x,判断f1(x),f2(x)是否在集合M中,并说明理由;
(II)求证:对任意的实数t,f(x)=
| -x+t | x2+1 |
(Ⅲ)是否存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,并且有相同的单调区间?请说明理由.
分析:(I)对于函数f1(x)=
,结合函数的图象可知f1(x)∈M;由于f2′(x)=3(x-1)2≥0,则f2(x)∉M;
(II)按照集合M满足的条件只需证明两条:①在定义域为R;②存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减;
(Ⅲ)假设存在满足条件的可导函数f(x),验证f(x)与g(x)=f′(x)-x是否有相同的单调区间即可.
|
(II)按照集合M满足的条件只需证明两条:①在定义域为R;②存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减;
(Ⅲ)假设存在满足条件的可导函数f(x),验证f(x)与g(x)=f′(x)-x是否有相同的单调区间即可.
解答: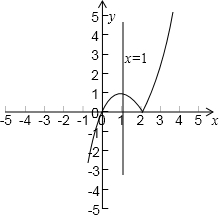 解:(I)对于函数f1(x)=
解:(I)对于函数f1(x)=
,满足:①f(x)定义域R,②f(x)在(-∞,1),(2,+∞)内单调递增,在(1,2)内单调递减,故f1(x)∈M;
对于函数f2(x)=x3-3x2+3x,由于f2′(x)=3x2-6x+3=3(x-1)2≥0,
故f2(x)=x3-3x2+3x在R上为增函数,故f2(x)∉M;
(II)证明:由题意知,f(x)=
的定义域为R,且f′(x)=
由于h(x)=x2-2tx-1的△=(-2t)2-4×1×(-1)=4t2+4>0恒成立,
故f′(x)=
恒有两个零点,即f(x)=
满足:存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减
故对任意的实数t,f(x)=
都在集合M中;
(Ⅲ)假设存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,
则f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减,故f'(x)<0的解集是(a,b)
则g(x)=f'(x)-x=(x-a)(x-b)-x为二次函数不满足:存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减,
故不存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,并且有相同的单调区间.
 解:(I)对于函数f1(x)=
解:(I)对于函数f1(x)=
|
对于函数f2(x)=x3-3x2+3x,由于f2′(x)=3x2-6x+3=3(x-1)2≥0,
故f2(x)=x3-3x2+3x在R上为增函数,故f2(x)∉M;
(II)证明:由题意知,f(x)=
| -x+t |
| x2+1 |
| x2-2tx-1 |
| (x2+1)2 |
由于h(x)=x2-2tx-1的△=(-2t)2-4×1×(-1)=4t2+4>0恒成立,
故f′(x)=
| x2-2tx-1 |
| (x2+1)2 |
| -x+t |
| x2+1 |
故对任意的实数t,f(x)=
| -x+t |
| x2+1 |
(Ⅲ)假设存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,
则f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减,故f'(x)<0的解集是(a,b)
则g(x)=f'(x)-x=(x-a)(x-b)-x为二次函数不满足:存在a<b,使f(x)在(-∞,a),(b,+∞)上分别单调递增,在(a,b)上单调递减,
故不存在可导函数f(x),使得f(x)与g(x)=f'(x)-x都在集合M中,并且有相同的单调区间.
点评:本题考查新定义,考查导数知识的运用,解题的关键是理解新定义,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 都在集合M中;
都在集合M中;