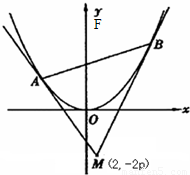
题目内容
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且 ,过A、B两点分别作抛物线的切线,设其交点为M
,过A、B两点分别作抛物线的切线,设其交点为M(1)证明线段FM被x轴平分;
(2)计算
 的值;
的值;(3)求证|FM|2=|FA|•|FB|.
【答案】分析:(1)设 ,由导数的几何意义可求直线AM的方程为:
,由导数的几何意义可求直线AM的方程为: ,直线BM的方程为:
,直线BM的方程为: ,解方程可求M,由已知A,B,F三点共线,设直线AB的方程为:y=kx+2,联立直线与抛物线方程,根据方程的根与系数关系可求线段FM中点的纵坐标O,可证
,解方程可求M,由已知A,B,F三点共线,设直线AB的方程为:y=kx+2,联立直线与抛物线方程,根据方程的根与系数关系可求线段FM中点的纵坐标O,可证
(2)由 ,利用向量的数量积,结合方程的根与系数的关系可求
,利用向量的数量积,结合方程的根与系数的关系可求
(3)由向量的数量积的性质可知 ,即AM⊥MB,而 MF⊥AB,在直角△MAB中,利用射影定理可证
,即AM⊥MB,而 MF⊥AB,在直角△MAB中,利用射影定理可证
解答:证明:(1)设 ,由
,由 得
得
直线AM的方程为:
直线BM的方程为:
解方程组得 即M(
即M( )(3分)
)(3分)
由已知 可得A,A,B,F三点共线,设直线AB的方程为:y=kx+2
可得A,A,B,F三点共线,设直线AB的方程为:y=kx+2
与抛物线方程x2=8y联立消y可得:x2-8kx-16=0
∴x1+x2=8k,x1x2=-16(5分)
∴ 即M点的纵坐标为-2,
即M点的纵坐标为-2,
∵F(0,2)
所以线段FM中点的纵坐标O
即线段FM被x轴平分. (6分)
解(2)∵F(0,2),M(4k,-2), ,
,
∴
∴
= =0 (9分)
=0 (9分)
证明:
∵ =
= =-8+4+4=0(13分)
=-8+4+4=0(13分)
∴ ,而 MF⊥AB所以在直角△MAB中,
,而 MF⊥AB所以在直角△MAB中,
由影射定理即得|FM|2=|FA|•|FB|(15分)
点评:本题主要考查了直线与直线与抛物线的相交关系的应用,向量数量积的坐标表示的应用,直角三角形的射影定理的应用,属于知识的综合应用.
 ,由导数的几何意义可求直线AM的方程为:
,由导数的几何意义可求直线AM的方程为: ,直线BM的方程为:
,直线BM的方程为: ,解方程可求M,由已知A,B,F三点共线,设直线AB的方程为:y=kx+2,联立直线与抛物线方程,根据方程的根与系数关系可求线段FM中点的纵坐标O,可证
,解方程可求M,由已知A,B,F三点共线,设直线AB的方程为:y=kx+2,联立直线与抛物线方程,根据方程的根与系数关系可求线段FM中点的纵坐标O,可证(2)由
 ,利用向量的数量积,结合方程的根与系数的关系可求
,利用向量的数量积,结合方程的根与系数的关系可求(3)由向量的数量积的性质可知
 ,即AM⊥MB,而 MF⊥AB,在直角△MAB中,利用射影定理可证
,即AM⊥MB,而 MF⊥AB,在直角△MAB中,利用射影定理可证解答:证明:(1)设
 ,由
,由 得
得
直线AM的方程为:

直线BM的方程为:

解方程组得
 即M(
即M( )(3分)
)(3分) 由已知
 可得A,A,B,F三点共线,设直线AB的方程为:y=kx+2
可得A,A,B,F三点共线,设直线AB的方程为:y=kx+2与抛物线方程x2=8y联立消y可得:x2-8kx-16=0
∴x1+x2=8k,x1x2=-16(5分)
∴
 即M点的纵坐标为-2,
即M点的纵坐标为-2,∵F(0,2)
所以线段FM中点的纵坐标O
即线段FM被x轴平分. (6分)
解(2)∵F(0,2),M(4k,-2),
 ,
,∴

∴

=
 =0 (9分)
=0 (9分)证明:

∵
 =
= =-8+4+4=0(13分)
=-8+4+4=0(13分)∴
 ,而 MF⊥AB所以在直角△MAB中,
,而 MF⊥AB所以在直角△MAB中,由影射定理即得|FM|2=|FA|•|FB|(15分)
点评:本题主要考查了直线与直线与抛物线的相交关系的应用,向量数量积的坐标表示的应用,直角三角形的射影定理的应用,属于知识的综合应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
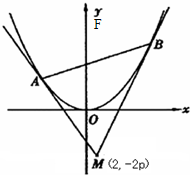 已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且 已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且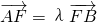 (λ>0),
(λ>0),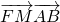 的值;
的值;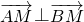 .
.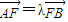 (λ>0),
(λ>0),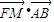 的值;
的值;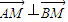 .
.