题目内容
已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于D,点D的坐标为(2,1),则p的值为( )
分析:设A(x1,y1),B(x2,y2),由直线OD斜率为
,OD⊥AB,知直线AB方程为2x+y-5=0,代入抛物线方程得y2+py-5p=0,从而得到y1y2=-5p,再由OA⊥OB,能求出p.
| 1 |
| 2 |
解答:解:设A(x1,y1),B(x2,y2),
∵直线OD斜率为
,OD⊥AB,∴直线AB斜率为-2,
故直线AB方程为2x+y-5=0…(1)
将(1)代入抛物线方程得y2+py-5p=0,
则y1y2=-5p,
∵y12=2px1,y22=2px2,
则(y1y2)2=4p2x1x2,
故x1x2=
,
∵OA⊥OB
∴x1x2+y1y2=0,
∵p>0,∴p=
.
故选C.
∵直线OD斜率为
| 1 |
| 2 |
故直线AB方程为2x+y-5=0…(1)
将(1)代入抛物线方程得y2+py-5p=0,
则y1y2=-5p,
∵y12=2px1,y22=2px2,
则(y1y2)2=4p2x1x2,
故x1x2=
| 25 |
| 4 |
∵OA⊥OB
∴x1x2+y1y2=0,
∵p>0,∴p=
| 5 |
| 4 |
故选C.
点评:本题考查直线与抛物线的位置关系的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
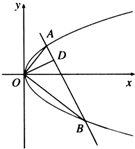 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1),求p的值.




