题目内容
设单位向量
、
夹角是60°，
=
+
，
=
+t
，若
、
夹角为锐角，则t的取值范围是（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
分析：由条件可得
•
=
，若
、
夹角为锐角，则有
•
＞0①，且
与
不共线②．由①求得t的范围，由②可得t≠1．综合可得t的取值范围．
| e1 |
| e2 |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：由单位向量
、
夹角是60°，可得
•
=1×1×cos60°=
，
若
、
夹角为锐角，则有
•
＞0①，且
与
不共线②．
由①可得 1+
+t＞0，解得 t＞-1．
由②可得 1•t-1×1≠0，解得t≠1．
综合可得，t的取值范围为t＞-1 且t≠1，
故选A．
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
若
| a |
| b |
| a |
| b |
| a |
| b |
由①可得 1+
| 1+t |
| 2 |
由②可得 1•t-1×1≠0，解得t≠1．
综合可得，t的取值范围为t＞-1 且t≠1，
故选A．
点评：本题主要考查用数量积表示两个两个向量的夹角，两个向量共线的性质，体现了转化的数学思想，属于
中档题．
中档题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
设单位向量
，
的夹角为60°，则向量3
+4
与向量
的夹角的余弦值是（ ）
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
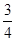B.
C.
D.