题目内容
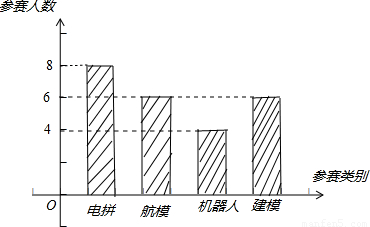
“知识改变命运,科技繁荣祖国”.大渡口区中小学每年都要举办一届科技比赛.如图为94中2013年将参加科技比赛(包括电拼、航模、机器人、建模四个类别)的参赛人数统计图.(1)我校参加机器人、建模比赛的人数分别是______人和______人;
(2)我校参加科技比赛的总人数是______人,电子百拼所在扇形的圆心角的度数
是______°,并把条形统计图补充完整;
(3)若电拼参赛票仅剩下一张,而仲镜霖和田宏铮两位同学都想要参加,于是波波老师决定采用抽扑克牌的方法来确定,规则是:“将同一副牌中正面分别标有数字1,2,3,4的四张牌洗匀后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一人抽后记下数字,将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若抽出的两次数字之积为偶数则仲镜霖获得门票,反之田宏铮获得门票.”请用画树状图或列表的方法计算出仲镜霖和田宏铮获得门票的概率,并说明这个规则对双方是否公平.
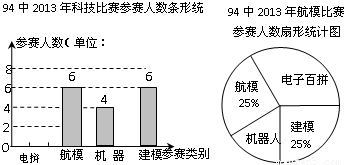
【答案】分析:(1)由参赛人数统计图可得,我校参加机器人、建模比赛的人数分别是4、6.
(2)根据参加航模比赛的人数为6,占的比例为 ,可得我校参加科技比赛的总人数.由此求得参加机器人比赛的人数所占的比例为
,可得我校参加科技比赛的总人数.由此求得参加机器人比赛的人数所占的比例为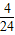 ,用电子百拼
,用电子百拼
所占的比例乘以360,即可得到电子百拼所在扇形的圆心角的度数.再根据参加电子百拼的人数为 24×(1-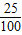 -
- -
- ),由此可把条形统计图补充完整.
),由此可把条形统计图补充完整.
(3)设仲镜霖和田宏铮二人抽取的数字分别为x、y,则所有的(x,y)共有4×4=16个,其中,满足x+y为偶数的(x,y)有6个,可得仲镜霖获得门票
的概率为 =
= ,故此二人获胜的概率不相等,故此游戏不公平.
,故此二人获胜的概率不相等,故此游戏不公平.
解答:解:(1)由参赛人数统计图可得,我校参加机器人、建模比赛的人数分别是4、6,
故答案为 4、6.
(2)根据参加航模比赛的人数为6,占的比例为 ,可得我校参加科技比赛的总人数是24.
,可得我校参加科技比赛的总人数是24.
由此求得参加机器人比赛的人数所占的比例为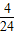 =
= ,故电子百拼所在扇形的圆心角的度数为 (1-
,故电子百拼所在扇形的圆心角的度数为 (1- -
-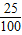 -
- )×360°=120°,
)×360°=120°,
故答案为 24、120.
参加电子百拼的人数为 24×(1-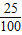 -
- -
- )=8,由此可把条形统计图补充完整如图所示:
)=8,由此可把条形统计图补充完整如图所示:
(3)设仲镜霖和田宏铮二人抽取的数字分别为x、y,则所有的(x,y)共有4×4=16个,
其中,满足x+y为偶数的(x,y)有:(1,1)、(1,3)、(2,2)、(2,4)、(3,1)、(3,3),共计6个,
故仲镜霖获得门票的概率为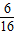 =
= <
< ,故田宏铮获得门票的概率为1-
,故田宏铮获得门票的概率为1- =
= >
> ,
,
故此二人获胜的概率不相等,故此游戏不公平.
点评:本题主要考查等可能事件的概率,频率分布直方图的应用,属于中档题.
(2)根据参加航模比赛的人数为6,占的比例为
 ,可得我校参加科技比赛的总人数.由此求得参加机器人比赛的人数所占的比例为
,可得我校参加科技比赛的总人数.由此求得参加机器人比赛的人数所占的比例为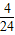 ,用电子百拼
,用电子百拼所占的比例乘以360,即可得到电子百拼所在扇形的圆心角的度数.再根据参加电子百拼的人数为 24×(1-
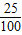 -
- -
- ),由此可把条形统计图补充完整.
),由此可把条形统计图补充完整.(3)设仲镜霖和田宏铮二人抽取的数字分别为x、y,则所有的(x,y)共有4×4=16个,其中,满足x+y为偶数的(x,y)有6个,可得仲镜霖获得门票
的概率为
 =
= ,故此二人获胜的概率不相等,故此游戏不公平.
,故此二人获胜的概率不相等,故此游戏不公平.解答:解:(1)由参赛人数统计图可得,我校参加机器人、建模比赛的人数分别是4、6,
故答案为 4、6.
(2)根据参加航模比赛的人数为6,占的比例为
 ,可得我校参加科技比赛的总人数是24.
,可得我校参加科技比赛的总人数是24.由此求得参加机器人比赛的人数所占的比例为
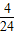 =
= ,故电子百拼所在扇形的圆心角的度数为 (1-
,故电子百拼所在扇形的圆心角的度数为 (1- -
-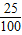 -
- )×360°=120°,
)×360°=120°,故答案为 24、120.
参加电子百拼的人数为 24×(1-
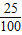 -
- -
- )=8,由此可把条形统计图补充完整如图所示:
)=8,由此可把条形统计图补充完整如图所示:
(3)设仲镜霖和田宏铮二人抽取的数字分别为x、y,则所有的(x,y)共有4×4=16个,
其中,满足x+y为偶数的(x,y)有:(1,1)、(1,3)、(2,2)、(2,4)、(3,1)、(3,3),共计6个,
故仲镜霖获得门票的概率为
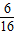 =
= <
< ,故田宏铮获得门票的概率为1-
,故田宏铮获得门票的概率为1- =
= >
> ,
,故此二人获胜的概率不相等,故此游戏不公平.
点评:本题主要考查等可能事件的概率,频率分布直方图的应用,属于中档题.

练习册系列答案
相关题目
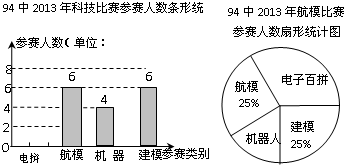 “知识改变命运,科技繁荣祖国”.大渡口区中小学每年都要举办一届科技比赛.如图为94中2013年将参加科技比赛(包括电拼、航模、机器人、建模四个类别)的参赛人数统计图.
“知识改变命运,科技繁荣祖国”.大渡口区中小学每年都要举办一届科技比赛.如图为94中2013年将参加科技比赛(包括电拼、航模、机器人、建模四个类别)的参赛人数统计图.