题目内容
16．设f（x）是R上的奇函数，且当x∈（0，+∞）时，f（x）=x2-1，则当x∈（-∞，0）时，f（x）=（ ）| A． | x2+1 | B． | x2-1 | C． | -x2+1 | D． | -x2-1 |
分析 当x∈（-∞，0）时，-x∈（0，+∞），此时f（x）=-f（-x），代入可得答案．
解答 解：∵设f（x）是R上的奇函数，当x∈（0，+∞）时，f（x）=x2-1，
又∵当x∈（-∞，0）时，-x∈（0，+∞），
∴f（x）=-f（-x）=-[（-x）2-1=-x2+1，
故选：C
点评 本题考查的知识点是函数奇偶性的性质，熟练掌握函数奇偶性的性质，是解答的关键．
练习册系列答案
相关题目
6．
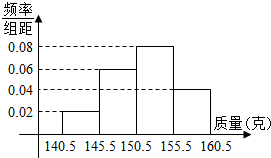为了了解某种进口茶叶的质量（单位：克），从中抽取若干包进行检查，获得样本的频率分布直方图如图所示．若已知样本中质量在[155.5，160.5）内的茶叶有10包，则样本容量为（ ）
为了了解某种进口茶叶的质量（单位：克），从中抽取若干包进行检查，获得样本的频率分布直方图如图所示．若已知样本中质量在[155.5，160.5）内的茶叶有10包，则样本容量为（ ）| A． | 150 | B． | 100 | C． | 70 | D． | 50 |
4．已知函数f（x）=$\left\{\begin{array}{l}{a•{2}^{x}，x≥0}\\{lo{g}_{2}（-x+3），x＜0}\end{array}\right.$（a∈R），若f[f（-1）]=1，则a=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
11．${2^{\frac{3}{4}}}$化成根式形式为（ ）
| A． | $\root{3}{2^4}$ | B． | $\root{4}{3^2}$ | C． | $\root{4}{2^3}$ | D． | $\root{2}{4^3}$ |
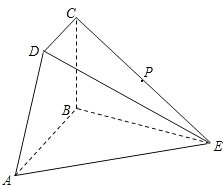如图所示，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，△ABE为等边三角形，且平面ABCD⊥平面ABE，AB=2CD=2BC=2，P为CE中点．