题目内容
已知 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,外接圆半径是
,外接圆半径是 ,,且满足条件
,,且满足条件 ,则
,则 的面积的最大值为 ( )
的面积的最大值为 ( )
A. | B. | C. | D. |
C
解析试题分析:由正弦定理可得b=2RsinB=2sinB,代入 得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
又由正弦定理得:a2+b2-c2=ab,∴cosC=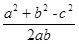
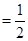 ,又C为三角形的内角,所以C=60°.
,又C为三角形的内角,所以C=60°.
因为ab=a2+b2-c2=a2+b2-(2rsinC)2=a2+b2-3≥2ab-3,所以ab≤3 (当且仅当a=b时,取等号),
所以△ABC面积为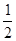 absinC≤
absinC≤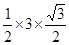 =
= 。
。
考点:本题考查正弦定理;余弦定理;三角形的面积公式;三角函数中的恒等变换;基本不等式的应用。
点评:本题的主要思路是:由ab=a2+b2-3≥2ab-3 求得ab最大值为3,从而求得△ABC面积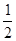 absinC 的最大值.其中求出ab≤3是解题的难点.
absinC 的最大值.其中求出ab≤3是解题的难点.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
要得到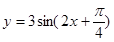 的图象只需将y=3sin2x的图象( )
的图象只需将y=3sin2x的图象( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向右平移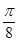 个单位 个单位 | D.向左平移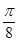 个单位 个单位 |
定义在R上的偶函数 在
在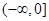 上是减函数,
上是减函数,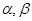 是钝角三角形的两个锐角,则下列不等式关系中正确的是( )
是钝角三角形的两个锐角,则下列不等式关系中正确的是( )
A.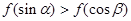 | B.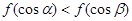 |
C. | D.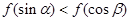 |
在同一平面直角坐标系中,函数y=cos(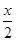 +
+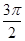 )(x∈[0,2π])的图象和直线y=
)(x∈[0,2π])的图象和直线y=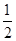 的交点个数是( )
的交点个数是( )
| A.0 | B.1 | C.2 | D.4 |
和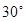 终边在同一条直线上的角的集合是( )
终边在同一条直线上的角的集合是( )
A.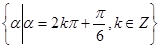 | B.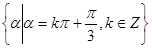 |
C.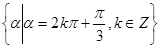 | D.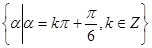 |
锐角△ABC中,若A=2B,则 的取值范围是( )
的取值范围是( )
| A.(1,2) | B.(1, ) ) | C.( ) ) | D.(  ) ) |
锐角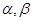 使
使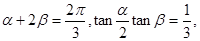 同时成立,则
同时成立,则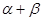 的值为( )
的值为( )
A.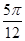 | B.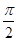 | C.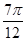 | D.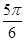 |
函数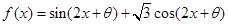 为奇函数,且在
为奇函数,且在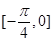 上为减函数的
上为减函数的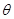 值可以是【 】
值可以是【 】
A.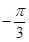 | B.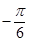 |
C.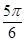 | D. |
 的图像为C,如下结论中正确的是( )
的图像为C,如下结论中正确的是( )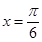 对称
对称  对称
对称 在区间
在区间 内是增函数
内是增函数 的图像向右平移
的图像向右平移 个单位长度可以得到图像C。
个单位长度可以得到图像C。