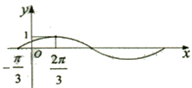
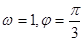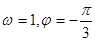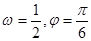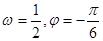题目内容
定义在R上的偶函数 在
在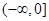 上是减函数,
上是减函数,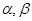 是钝角三角形的两个锐角,则下列不等式关系中正确的是( )
是钝角三角形的两个锐角,则下列不等式关系中正确的是( )
A.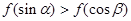 | B.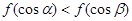 |
C. | D.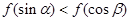 |
D
解析试题分析:因为α,β是钝角三角形的两个锐角,所以0°<α+β<90°,即0°<α<90°-β,所以0<sinα<sin(90°-β)=cosβ<1,因为定义在R上的偶函数 在
在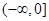 上是减函数,所以
上是减函数,所以 在
在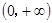 上单调递增。所以
上单调递增。所以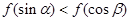
考点:本题考查函数的奇偶性;诱导公式;函数的单调性。
点评:本题的关键有两条:关键一是要熟练掌握偶函数在对称区间上的单调性相反的性质;关键二是由α,β是钝角三角形的两个锐角可得0°<α+β<90°即0°<α<90°-β.本题是综合性较好的试题。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知 ,函数
,函数 在
在 上单调递减.则
上单调递减.则 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
若角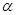 和角
和角 的终边关于
的终边关于 轴对称,则
轴对称,则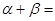 ( )
( )
A.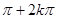 , ,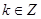 | B.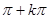 , ,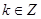 |
C.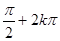 , ,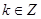 | D. , ,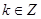 |
若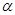 为第三象限角,则
为第三象限角,则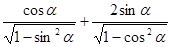 的值为 ( )
的值为 ( )
| A.-3 | B.-1 | C.1 | D.3 |
函数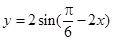 (
(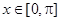 )的单调递增区间是( ).
)的单调递增区间是( ).
A.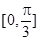 | B.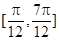 | C.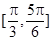 | D.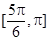 |
若函数 的取值分别是( )
的取值分别是( )
A. | B. |
C. | D. |
已知 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,外接圆半径是
,外接圆半径是 ,,且满足条件
,,且满足条件 ,则
,则 的面积的最大值为 ( )
的面积的最大值为 ( )
A. | B. | C. | D. |
若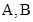 为锐角三角形
为锐角三角形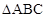 的两个内角,则点
的两个内角,则点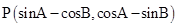
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
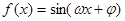 的图象(部分)如图所示,则
的图象(部分)如图所示,则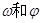 的取值是 ( )
的取值是 ( )