题目内容
下列命题中,真命题是(1)4≥3; (2)4≥4; (3)?x∈Q,x2-8=0; (4)?x∈R,x2+2>0.
分析:因为大于等于号只要有一个正确就可以,故(1)(2)是真命题,根据x2-8=0时,有x=±2
,得到不存在x∈Q,
x2-8=0; 根据x2+2>0恒成立,得到?x∈R,x2+2>0.得到结果.
| 2 |
x2-8=0; 根据x2+2>0恒成立,得到?x∈R,x2+2>0.得到结果.
解答:解:4≥3和4≥4都正确,因为大于等于号只要有一个正确就可以,故(1)(2)是真命题,
∵x2-8=0时,x=±2
,∴不存在x∈Q,x2-8=0;故(3)不正确
∵x2+2>0恒成立,∴?x∈R,x2+2>0.故(4)正确,
故答案为:(1)(2)(4)
∵x2-8=0时,x=±2
| 2 |
∵x2+2>0恒成立,∴?x∈R,x2+2>0.故(4)正确,
故答案为:(1)(2)(4)
点评:本题考查复合命题的真假,包括不等式成立的条件,考查全称命题和特称命题的真假,是一个比较简单的综合题目,这种题目比较容易做对.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
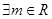 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1