题目内容
已知正方形的中心为点M(-1,0),一条边所在的直线为l1:3x-y-3=0,求正方形其它三边所在的直线方程.
M(-1,0)到直线3x-y-3=0的距离是
=
,
所以M到另三边距离也是
,其中有一条边和3x-y-3=0平行
设为3x-y+c=0,由
=
,解得c=9或c=-3(舍去)
故方程为3x-y+9=0
另两条和他们垂直,所以斜率为-
设为:x+3y+b=0,由
=
,解得b=-5或b=7
故所求直线方程为:x+3y-5=0,x+3y+7=0,
故正方形其它三边所在的直线方程为:3x-y+9=0,x+3y-5=0,x+3y+7=0
| |-3-3| | ||
|
3
| ||
| 5 |
所以M到另三边距离也是
3
| ||
| 5 |
设为3x-y+c=0,由
| |-3+c| | ||
|
3
| ||
| 5 |
故方程为3x-y+9=0
另两条和他们垂直,所以斜率为-
| 1 |
| 3 |
设为:x+3y+b=0,由
| |-1+b| | ||
|
3
| ||
| 5 |
故所求直线方程为:x+3y-5=0,x+3y+7=0,
故正方形其它三边所在的直线方程为:3x-y+9=0,x+3y-5=0,x+3y+7=0

练习册系列答案
相关题目
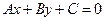 和坐标轴都相交,则有 。
和坐标轴都相交,则有 。