题目内容
15. 如图,一条东西走向的大江,其河岸A处有人要渡江到对岸B处,江面上有一座大桥AC,已知B在A的西南方向,C在A的南偏西15°,BC=10公里.现有两种渡江方案:
如图,一条东西走向的大江,其河岸A处有人要渡江到对岸B处,江面上有一座大桥AC,已知B在A的西南方向,C在A的南偏西15°,BC=10公里.现有两种渡江方案:方案一:开车从大桥AC渡江到C处,然后再到B处;
方案二:直接坐船从A处渡江到对岸B处.
若车速为每小时60公里,船速为每小时45公里(不考虑水流速度),为了尽快到达B处,应选择哪个方案?说明理由.
分析 分别计算两种方案的时间即可.
解答  解:如图,过A作AD垂直BC交于D,
解:如图,过A作AD垂直BC交于D,
根据题意知∠CAD=15°,∠BAD=45°,
设CD为x公里,则有AD=$\frac{CD}{tan15°}$,
由于tan15°=tan(45°-30°)
=$\frac{tan45°-tan30°}{1+tan45°tan30°}$=$\frac{1-\frac{\sqrt{3}}{3}}{1+1×\frac{\sqrt{3}}{3}}$=$\frac{3-\sqrt{3}}{3+\sqrt{3}}$=$2-\sqrt{3}$,
故AD=$\frac{CD}{tan15°}$=$\frac{x}{2-\sqrt{3}}$=(2$+\sqrt{3}$)x,
∵BC=10公里,∠BAD=45°,∴BD=AD,
即(2$+\sqrt{3}$)x=x+10,解得x=CD=$5\sqrt{3}-5$,
从而AD=(2$+\sqrt{3}$)×($5\sqrt{3}-5$)=5+$5\sqrt{3}$,
AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{(5\sqrt{3}-5)^{2}+(5+5\sqrt{3})^{2}}$=10$\sqrt{2}$≈14.14,
AB=$\sqrt{2}AD$=$\sqrt{2}×$(5+$5\sqrt{3}$)=$5\sqrt{2}(\sqrt{3}+1)$≈19.32,
下面分别计算两种方案所要花费的时间:
方案一:$\frac{AC+BC}{60}$≈$\frac{14.14+10}{60}$≈0.4023(时);
方案二:$\frac{AB}{45}$$≈\frac{19.32}{45}$≈0.4293(时);
显然选择方案一.
点评 本题考查速度、路程、时间之间的关系,属于基础题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )
如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
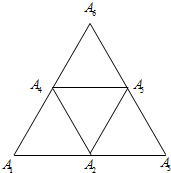 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )| A. | {-2,-1,0,1,2} | B. | $\left\{{-2,-1,-\frac{1}{2},0,\frac{1}{2},1,2}\right\}$ | ||
| C. | $\left\{{-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}}\right\}$ | D. | $\left\{{-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2},2}\right\}$ |
 如图所示的圆内接四边形ABCD中,∠ABC>$\frac{π}{2}$,∠ADB=∠CDB,DB交AC于点E.若△ADC的面积S=$\frac{\sqrt{3}}{4}$DE•DB,则∠ADC的大小为$\frac{π}{3}$.
如图所示的圆内接四边形ABCD中,∠ABC>$\frac{π}{2}$,∠ADB=∠CDB,DB交AC于点E.若△ADC的面积S=$\frac{\sqrt{3}}{4}$DE•DB,则∠ADC的大小为$\frac{π}{3}$.