题目内容
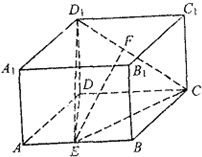 (2009•大连二模)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E、F分别为线段AB、D1C的中点.
(2009•大连二模)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,E、F分别为线段AB、D1C的中点.(I)求证:EF∥平面A1D;
(II)求V E-ADD1A1:VE-CDD1的值.
分析:(Ⅰ)取DD1的中点G,连结FG、AG,证明四边形AEFG为平行四边形,利用直线与平面平行的判定定理证明EF∥平面A1D;
(II)通过体积公式直接求V E-ADD1A1与VE-CDD1的体积然后求解比值.
(II)通过体积公式直接求V E-ADD1A1与VE-CDD1的体积然后求解比值.
解答:证明:(Ⅰ)取DD1的中点G,连结FG、AG,
依题意可知:GF是△CDD1的中位线,
则 GF∥
DC且GF=
DC,
AE∥
DC 且AE=
DC,
所以GF∥AE,且GF=AE,即四边形AEFG为平行四边形,…(3分)
则EF∥AG,又AG?平面AD1,EF?平面AD1,
所以EF∥平面AD1.…(6分)
(Ⅱ)解:V E-ADD1A1=
SADD1A1×AE=
SABCD×AE=
×1×1×1=
.
VE-CDD1=
SCDD1×AD=
×
×1×2×1=
.
V E-ADD1A1:VE-CDD1=1
∴V E-ADD1A1:VE-CDD1的值为1.…(12分)
依题意可知:GF是△CDD1的中位线,
则 GF∥
| 1 |
| 2 |
| 1 |
| 2 |
AE∥
| 1 |
| 2 |
| 1 |
| 2 |
所以GF∥AE,且GF=AE,即四边形AEFG为平行四边形,…(3分)
则EF∥AG,又AG?平面AD1,EF?平面AD1,
所以EF∥平面AD1.…(6分)
(Ⅱ)解:V E-ADD1A1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
VE-CDD1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
V E-ADD1A1:VE-CDD1=1
∴V E-ADD1A1:VE-CDD1的值为1.…(12分)
点评:本题考查直线与平面平行的判定定理的应用,几何体是体积的求法,考查计算能力.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 (2009•大连二模)如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是( )
(2009•大连二模)如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形S内部的概率是( )