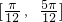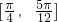题目内容
(文科做)已知O为坐标原点,圆心为M的圆的参数方程为
(θ∈R),点N为圆M上的任意一点,则<
,
>的取值范围是( )
|
| OM |
| ON |
分析:由圆的参数方程
(θ∈R)得圆心M(2,2),半径r=
,点N为圆M上的任意一点,
与
共线同向时,<
,
>最小,为0,当
与圆相切时,<
,
>最大,在直角三角形ONM中即可解决.
|
| 2 |
| OM |
| ON |
| OM |
| ON |
| ON |
| OM |
| ON |
解答:解:由圆的参数方程
(θ∈R)得圆心M(2,2),半径r=
,又点N为圆M上的任意一点,
∴当
与
共线同向时,<
,
>最小,为0;
当
与圆相切时,<
,
>最大,而三角形ONM为直角三角形,其中,
=2
,|MN|=r=
,
∴sin<
,
> max=
=
,
∴<
,
>max=
.
故选C.
|
| 2 |
∴当
| OM |
| ON |
| OM |
| ON |
当
| ON |
| OM |
| ON |
| |OM| |
| 2 |
| 2 |
∴sin<
| OM |
| ON |
| ||
2
|
| 1 |
| 2 |
∴<
| OM |
| ON |
| π |
| 6 |
故选C.
点评:本题考查数量积表示两个向量的夹角,关键是理解题意,将
与
的夹角问题分(共线与不共线)两类讨论解决,注意转化思想与方程思想的考查,属于中档题.
| OM |
| ON |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ,则<
,则< >的取值范围是
>的取值范围是