题目内容
对任意的函数f(x),g(x),在公共定义域内,规定f(x)*g(x)=minf(x),g(x),若f(x)=6-x,g(x)=| x |
分析:在同一个坐标系中作出两函数的图象,横坐标一样时取函数值较小的那一个,如图,由图象可以看出,最大值是2.
解答:解:∵f(x)*g(x)=min{f(x),g(x)},
∴f(x)*g(x)=min{6-x,
}的定义域为(0,+∞),
f(x)*g(x)=min{6-x,
}=
,画出其图象如图,由图象可知
f(x)*g(x)的最大值为 2,
故答案为:2.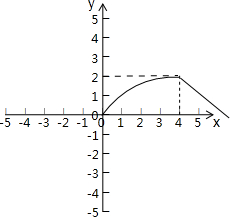
∴f(x)*g(x)=min{6-x,
| x |
f(x)*g(x)=min{6-x,
| x |
|
f(x)*g(x)的最大值为 2,
故答案为:2.
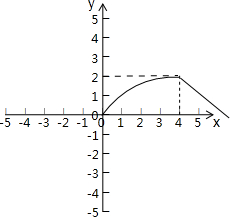
点评:本题考点是函数的最值及其几何意义,本题考查新定义,需要根据题目中所给的新定义作出相应的图象由图象直观观察出函数的最值,对于一些分段类的函数,其最值往往借助图象来解决.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
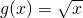 ,则f(x)*g(x)的最大值为________.
,则f(x)*g(x)的最大值为________.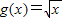 ,则f(x)*g(x)的最大值为 .
,则f(x)*g(x)的最大值为 .