题目内容
已知函数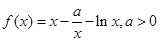 .
.
(I)讨论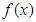 的单调性;
的单调性;
(Ⅱ)若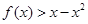 在(1,+
在(1,+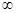 )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.
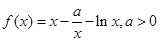 .
.(I)讨论
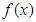 的单调性;
的单调性;(Ⅱ)若
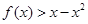 在(1,+
在(1,+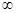 )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.(I)当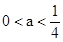 时,
时,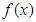 在
在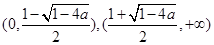 上是增函数.在
上是增函数.在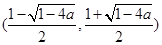 上是减函数.当
上是减函数.当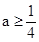 时,
时,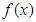 在
在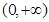 上是增函数.(II)
上是增函数.(II)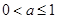 .
.
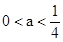 时,
时,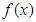 在
在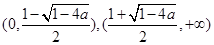 上是增函数.在
上是增函数.在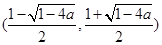 上是减函数.当
上是减函数.当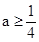 时,
时,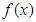 在
在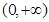 上是增函数.(II)
上是增函数.(II)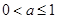 .
.试题分析:(I)首先应明确函数
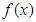 的定义域为
的定义域为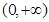 ,
,其次求导数,讨论①当
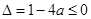 时,②当
时,②当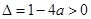 时,
时,导函数值的正负,求得函数的单调性.
(II)注意到
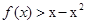 ,即
,即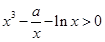 ,构造函数
,构造函数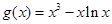 ,研究其单调性
,研究其单调性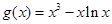 在
在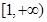 为增函数,从而由
为增函数,从而由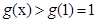 ,得到
,得到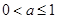 .
.试题解析:(I)函数
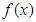 的定义域为
的定义域为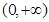 ,
,由于
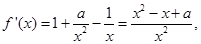
①当
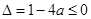 ,即
,即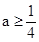 时,
时,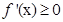 恒成立,
恒成立,所以
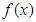 在
在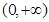 上都是增函数;
上都是增函数;②当
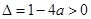 ,即
,即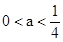 时,
时,由
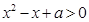 得
得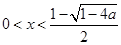 或
或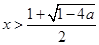 ,
,又由
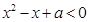 得
得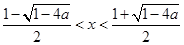 ,
,所以
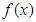 在
在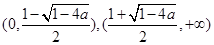 上是增函数.在
上是增函数.在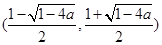 上是减函数.
上是减函数.综上知当
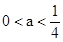 时,
时,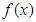 在
在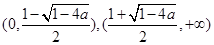 上是增函数.在
上是增函数.在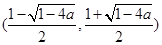 上是减函数.
上是减函数.当
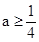 时,
时,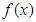 在
在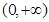 上是增函数.
上是增函数.(II)
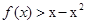 ,即
,即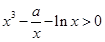 ,因为
,因为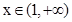 ,
,所以
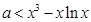
令
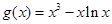 ,则
,则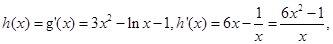
在
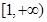 上,
上,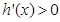 ,得
,得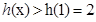 ,即
,即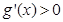 ,
,故
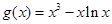 在
在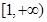 为增函数,
为增函数,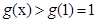 ,
,所以
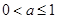 .
.
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
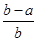 <ln
<ln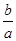 <
<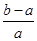 ,其中0<a<b;
,其中0<a<b;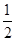 + +
+ +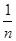 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).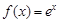 ,
,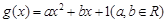 .
.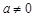 ,则
,则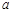 ,
,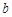 满足什么条件时,曲线
满足什么条件时,曲线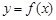 与
与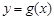 在
在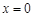 处总有相同的切线?
处总有相同的切线?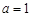 时,求函数
时,求函数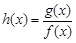 的单调减区间;
的单调减区间;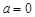 时,若
时,若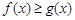 对任意的
对任意的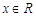 恒成立,求
恒成立,求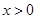 ,函数
,函数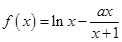 .
.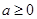 时,讨论函数
时,讨论函数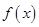 的单调性;
的单调性;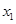 和
和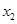 )时,求证:
)时,求证: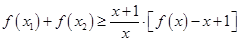 .
.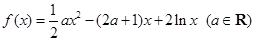 .
.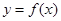 在
在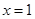 和
和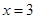 处的切线互相平行,求
处的切线互相平行,求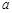 的值;
的值;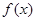 的单调区间;
的单调区间;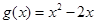 ,若对任意
,若对任意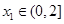 ,均存在
,均存在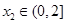 ,使得
,使得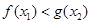 ,求
,求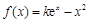 (其中
(其中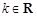 ,e是自然对数的底数).
,e是自然对数的底数).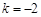 ,试判断函数
,试判断函数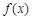 在区间
在区间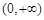 上的单调性;
上的单调性;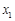 ,
,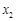 (
( ),求k的取值范围;
),求k的取值范围;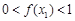 .
.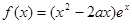 ,其中
,其中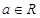 ,曲线
,曲线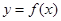 在点
在点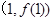 处的切线垂直于
处的切线垂直于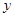 轴.
轴.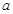 的值;
的值;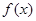 的极值.
的极值.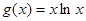 .
.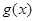 在
在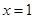 处的切线方程;
处的切线方程;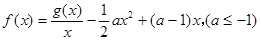 的单调区间;
的单调区间;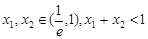 ,求证:
,求证: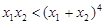 .
.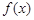 的导函数是
的导函数是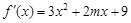 ,
,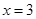 处取得极值,且
处取得极值,且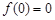 .
.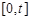 上的最大值为
上的最大值为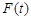 ,若对任意的
,若对任意的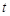
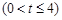 总有
总有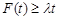 成立,求
成立,求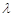 的取值范围;
的取值范围;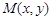 是曲线
是曲线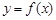 上的任意一点.当
上的任意一点.当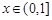 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断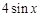 的大小关系,并说明理由.
的大小关系,并说明理由.