题目内容
求方程ax2+2x+1=0有且只有一个负实数根的充要条件
解:方程ax2+2x+1=0有且仅有一负根.
当a=0时,x=-适合条件.
当a≠0时,方程ax2+2x+1=0有实根,
则Δ=4-4a≥0,∴a≤1,
当a=1时,方程有一负根x=-1.
当a<1时,若方程有且仅有一负根,则<0,
∴a<0.
综上,方程ax2+2x+1=0有且仅有一负实数根的充要条件为a≤0或a=1.
当a=0时,x=-适合条件.
当a≠0时,方程ax2+2x+1=0有实根,
则Δ=4-4a≥0,∴a≤1,
当a=1时,方程有一负根x=-1.
当a<1时,若方程有且仅有一负根,则<0,
∴a<0.
综上,方程ax2+2x+1=0有且仅有一负实数根的充要条件为a≤0或a=1.
略

练习册系列答案
相关题目
 是等比数列,则
是等比数列,则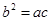 ”的逆命题
”的逆命题 ∥
∥ ,
,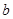 ∥
∥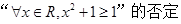

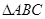 内接于以
内接于以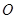 为圆心,1为半径的圆,且
为圆心,1为半径的圆,且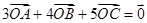 ,则
,则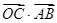 的值为( )
的值为( )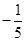
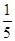
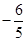
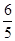
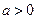 ,设命题
,设命题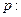 函数
函数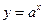 在R上单调递减,
在R上单调递减,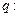 不等式
不等式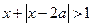 的解集为R,若
的解集为R,若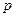 和
和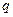 中有且只有一个命题为真命题,求
中有且只有一个命题为真命题,求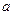 的取值范围.
的取值范围. ,
, ,
, ,
,
 ,
, ,
, ,
, 直线
直线
 ,
,
 、
、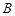 、
、 ,
, 且
且 不共线
不共线 、
、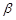 重合
重合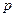 :实数
:实数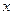 满足
满足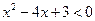 ,
,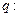 实数
实数 ,若
,若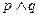 为真,求实数
为真,求实数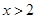 且
且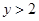 ”是“
”是“ ”的 ( )
”的 ( )