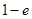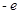题目内容
已知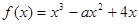 有两个极值点
有两个极值点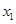 、
、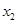 ,且
,且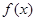 在区间(0,1)上有极大值,无极小值,则实数
在区间(0,1)上有极大值,无极小值,则实数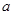 的取值范围是( )
的取值范围是( )
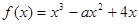 有两个极值点
有两个极值点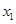 、
、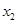 ,且
,且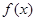 在区间(0,1)上有极大值,无极小值,则实数
在区间(0,1)上有极大值,无极小值,则实数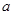 的取值范围是( )
的取值范围是( ) A.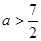 | B. | C.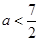 | D. |
A
试题分析:f′(x)=3x2-2ax+4,∵f(x)在区间(0,1)上有极大值,无极小值,
∴
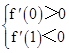 ,即3-2a+4<0,解得
,即3-2a+4<0,解得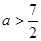 ,故选A。
,故选A。点评:中档题,利用导数研究函数的极值,遵循“求导数,求驻点,研究单调性,求极值”。

练习册系列答案
相关题目
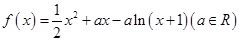 .
.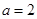 时,求函数
时,求函数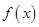 的极值;
的极值;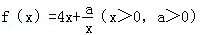 在x=3时取得最小值,则a= .
在x=3时取得最小值,则a= .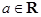 ,函数
,函数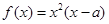 ,若
,若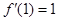 .
.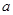 的值并求曲线
的值并求曲线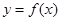 在点
在点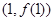 处的切线方程
处的切线方程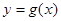 ;
;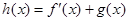 ,求
,求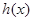 在
在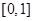 上的最大值与最小值.
上的最大值与最小值.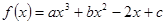 在
在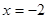 时有极大值6,在
时有极大值6,在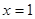 时有极小值,求
时有极小值,求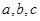 的值;并求
的值;并求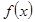 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.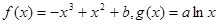 .
.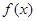 在
在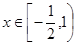 上的最大值为
上的最大值为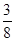 ,求实数
,求实数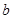 的值;
的值;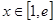 ,都有
,都有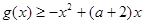 恒成立,求实数
恒成立,求实数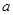 的取值范围;
的取值范围;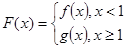 ,对任意给定的正实数
,对任意给定的正实数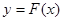 上是否存在两点
上是否存在两点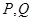 ,使得
,使得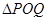 是以
是以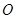 (
( 轴上?请说明理由.
轴上?请说明理由.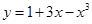 有( )
有( ) 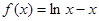 在区间
在区间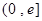 的最大值为( )
的最大值为( )