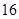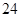题目内容
若直线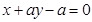 与直线
与直线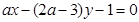 垂直,则
垂直,则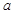 的值为 ( )
的值为 ( )
| A.2 | B.-3或1 | C.2或0 | D.1或0 |
C
解析试题分析:对于两条直线的垂直关系,我们可以将直线化为斜截式的形式,通过斜率是否互为负倒数,或者一个斜率不存在一个斜率为零来判定,或者结合一般式中的充要条件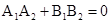 来判定。由于当a=0时,直线
来判定。由于当a=0时,直线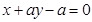 斜率不存在,此时直线
斜率不存在,此时直线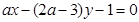 的方程为3y-1=0,可知其斜率为零符合题意,故a=0;其次就是当
的方程为3y-1=0,可知其斜率为零符合题意,故a=0;其次就是当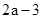 =0时,直线
=0时,直线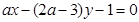 斜率不存在,而
斜率不存在,而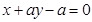 的斜率
的斜率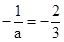 不为零,不符合舍去;,那么最后考虑斜率之积
不为零,不符合舍去;,那么最后考虑斜率之积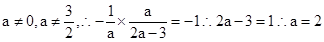 满足题意,故选C.
满足题意,故选C.
考点:本试题主要是考查了平面中两条直线的位置关系中垂直的判定。
点评:解决这类问题,最容易出错的地方就是丢情况,忽略了一条直线斜率不存在,一条直线斜率为0时的垂直。仅仅考虑斜率之积为-1.

练习册系列答案
相关题目
直线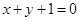 的倾斜角与其在
的倾斜角与其在 轴上的截距分别是 ( )
轴上的截距分别是 ( )
A.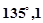 | B.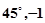 | C.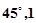 | D.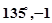 |
( )过点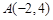 ,且在
,且在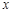 轴上截距是
轴上截距是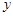 轴上截距的
轴上截距的 倍的直线方程为
倍的直线方程为
A.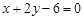 或 或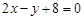 | B.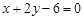 或 或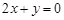 |
C.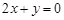 或 或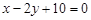 | D.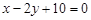 或 或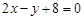 |
一束光线从点 出发经
出发经 轴反射到圆C:
轴反射到圆C: 上的最短路程是( )
上的最短路程是( )
| A.4 | B.5 | C.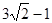 | D. |
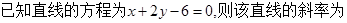 ( )
( )
A.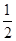 | B.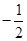 | C. | D.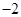 |
直线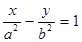 在
在 轴上的截距是( )
轴上的截距是( )
A.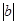 | B.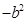 | C.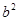 | D.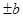 |
已知直线 平行,则k得值是( )
平行,则k得值是( )
| A. 1或3 | B.1或5 | C.3或5 | D.1或2 |
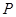 在直线
在直线 上
上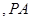 、
、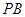 与圆
与圆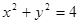 分别相切于
分别相切于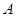 、
、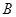 两点
两点 则四边形
则四边形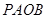 的面积的最小值为( )
的面积的最小值为( )