题目内容
 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.
 解:(1)证明:由直四棱柱,得BB1∥DD1且BB1=DD1,所以BB1D1D是平行四边形,
解:(1)证明:由直四棱柱,得BB1∥DD1且BB1=DD1,所以BB1D1D是平行四边形,所以B1D1∥BD.
而BD?平面A1BD,B1D1?平面A1BD,
所以B1D1∥平面A1BD.
(2)证明:因为BB1⊥面ABCD,AC?面ABCD,所以BB1⊥AC,
又因为BD⊥AC,且BD∩BB1=B,
所以AC⊥面BB1D,
而MD?面BB1D,所以MD⊥AC.
(3)当点M为棱BB1的中点时,平面DMC1⊥平面CC1D1D
取DC的中点N,D1C1的中点N1,连接NN1交DC1于O,连接OM.
因为N是DC中点,BD=BC,所以BN⊥DC;又因为DC是面ABCD与面DCC1D1的交线,而面ABCD⊥面DCC1D1,
所以BN⊥面DCC1D1.
又可证得,O是NN1的中点,所以BM∥ON且BM=ON,即BMON是平行四边形,所以BN∥OM,所以OM⊥平面CC1D1D,因为OM?面DMC1,所以平面DMC1⊥平面CC1D1D.
分析:(1)在平面A1BD内找到和B1D1平行的直线BD即可.利用线线平行来推线面平行.
(2)先利用条件BB1⊥AC和BD⊥AC证得AC⊥面BB1D,再证明MD⊥AC即可.
(3)因为棱BB1上最特殊的点是中点,所以先看中点.取DC的中点N,D1C1的中点N1,连接NN1交DC1于O,?BN⊥DC?面ABCD⊥面DCC1D1,
?BN⊥面DCC1D1.而又可证得BN∥OM,所以可得OM⊥平面CC1D1D?平面DMC1⊥平面CC1D1D.
点评:本题考查平面和平面垂直的判定和性质.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.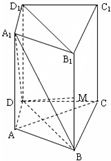 18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点.
18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点. 16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.
16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.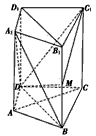
 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.