题目内容

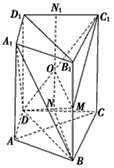
如图所示，在直四棱柱ABCD-A1B1C1D1中，DB=BC，DB⊥AC，点M是棱BB1上一点．
（1）求证：B1D1∥面A1BD；
（2）求证：MD⊥AC；
（3）试确定点M的位置，使得平面DMC1⊥平面CC1D1D。
（1）证明：由直四棱柱，得BB1∥DD1，且BB1=DD1，
所以，BB1D1D是平行四边形，
所以，B1D1∥BD，
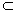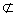而BD平面A1BD，B1D1平面A1BD，
所以B1D1∥平面A1BD．
（2）证明：因为BB1⊥面ABCD，AC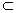面ABCD，
所以BB1⊥AC，
又因为BD⊥AC，且BD∩BB1=B，
所以，AC⊥面BB1D，
而M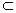D面BB1D，
所以MD⊥AC．
（3）解：当点M为棱BB1的中点时，平面DMC1⊥平面CC1D1D，
取DC的中点N，D1C1的中点N1，
连结NN1交DC1于O，连结OM，
因为N是DC中点，BD=BC，
所以，BN⊥DC；
又因为DC是面ABCD与 面DCC1D1的交线，
而面ABCD⊥面DCC1D1，
所以，BN⊥面DCC1D1，
又可证得，O是NN1的中点，
所以，BM∥ON且BM=ON，即BMON是平行四边形，
所以，BN∥OM，
所以，OM⊥平面CC1D1D，
因为OM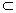面DMC1，
所以，平面DMC1⊥平面CC1D1D．
练习册系列答案
相关题目
19、如图所示，在直四棱柱ABCD-A1B1C1D1中，DB=BC，DB⊥AC，点M是棱BB1上一点．
（1）求证：B1D1∥面A1BD；
（2）求证：MD⊥AC；
（3）试确定点M的位置，使得平面DMC1⊥平面CC1D1D．
18、如图所示，在直四棱柱ABCD-A1B1C1D1中，DB⊥AC，点M是棱BB1上一点．
（1）求证：B1D1∥面A1BD；
（2）求证：MD⊥AC．
16、如图所示，在直四棱柱M中，DB=BC，MN，点EN是棱MN上一点．
（1）求证B1D1∥面A1BD；
（2）求证：MD⊥AC；
（3）试确定点M的位置，使得平面DMC1⊥平面CC1D1D．
如图所示，在直四棱柱ABCD-A1B1C1D1中，DB=BC，DB⊥AC，点M是棱BB1上一点．
（1）求证：B1D1∥面A1BD；
（2）求证：MD⊥AC；
（3）试确定点M的位置，使得平面DMC1⊥平面CC1D1D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网