题目内容
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料
，乙材料
.用5个工时；生产一件产品B需要甲材料
，乙材料
，用3个工时。生产一件产品A的利润为2100元，生产一件产品B的利润为900元，该企业现有甲材料150，乙材料
，则在不超过600个工时的条件下，生产产品A，产品B的利润之和的最大值为______________元.
【答案】216000元
【解析】设生产A产品x件，B产品y件，利润总和为z，
则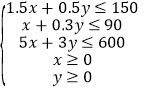
,目标函数z=2100x+900y，
做出可行域如图所示：
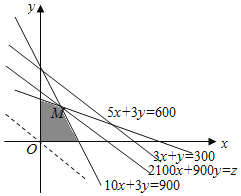
将z=2100x+900y变形，得
,
由图象可知，当直线经过点M时，z取得最大值．
解方程组
得M的坐标为（60，100）．
所以当x=60，y=100时，zmax=2100×60+900×100=216000．
故生产产品A、产品B的利润之和的最大值为216000元．
练习册系列答案
相关题目
【题目】某餐厅通过查阅了最近5次食品交易会参会人数
(万人)与餐厅所用原材料数量
(袋)，得到如下统计表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
（1）根据所给5组数据，求出
关于
的线性回归方程
.
（2）已知购买原材料的费用
(元)与数量
(袋)的关系为
，
投入使用的每袋原材料相应的销售收入为700元，多余的原材料只能无偿返还，据悉本次交易大会大约有15万人参加，根据(1)中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？(注：利润
销售收入
原材料费用).
参考公式： 
， 
.
参考数据： 
， 
， 
.
