题目内容
已知函数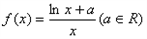 ,
,
(Ⅰ)求f(x)的极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间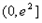 上有公共点,求实数a的取值范围;
上有公共点,求实数a的取值范围;
(Ⅲ)设各项为正的数列{an}满足:a1=1,an+1=lnan+an+2,n∈N*,求证:an≤2n-1。
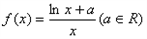 ,
,(Ⅰ)求f(x)的极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间
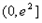 上有公共点,求实数a的取值范围;
上有公共点,求实数a的取值范围; (Ⅲ)设各项为正的数列{an}满足:a1=1,an+1=lnan+an+2,n∈N*,求证:an≤2n-1。
解:(Ⅰ)f(x)的定义域为(0,+∞),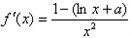 ,
,
令f′(x)=0得x=e1-a,
当 是增函数;
是增函数;
当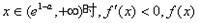 是减函数;
是减函数;
∴f(x)在x= 处取得极大值,
处取得极大值,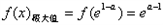 ,无极小值。
,无极小值。
(Ⅱ)①当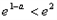 时,即a>-1时,
时,即a>-1时,
由(Ⅰ)知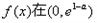 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
∴ ,
,
又当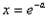 时,f(x)=0,
时,f(x)=0,

 时,
时, ,
,
∴f(x)与函数g(x)=1的图象在 上有公共点
上有公共点
 解得a≥1,
解得a≥1,
又a>-1,所以a≥1。
②当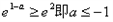 时,
时, 上是增函数,
上是增函数,
∴f(x)在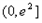 上的最大值为
上的最大值为 ,
,
所以原问题等价于
又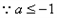 ,∴无解;
,∴无解;
综上,实数a的取值范围是 。
。
(Ⅲ)令a=1,由(Ⅰ)知,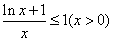 ,
,
∴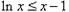 ,
,
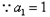 ,假设
,假设 ,
,
则 ,
,
故 ,
,
从而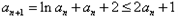 ,
,
∴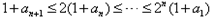 ,
,
即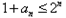 ,
,
∴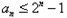 。
。
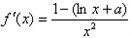 ,
,令f′(x)=0得x=e1-a,
当
 是增函数;
是增函数;当
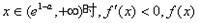 是减函数;
是减函数;∴f(x)在x=
 处取得极大值,
处取得极大值,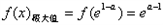 ,无极小值。
,无极小值。(Ⅱ)①当
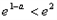 时,即a>-1时,
时,即a>-1时,由(Ⅰ)知
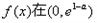 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,∴
 ,
,又当
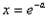 时,f(x)=0,
时,f(x)=0,
 时,
时, ,
,∴f(x)与函数g(x)=1的图象在
 上有公共点
上有公共点
 解得a≥1,
解得a≥1,又a>-1,所以a≥1。
②当
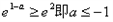 时,
时, 上是增函数,
上是增函数,∴f(x)在
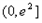 上的最大值为
上的最大值为 ,
,所以原问题等价于

又
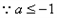 ,∴无解;
,∴无解;综上,实数a的取值范围是
 。
。(Ⅲ)令a=1,由(Ⅰ)知,
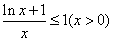 ,
,∴
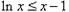 ,
,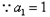 ,假设
,假设 ,
,则
 ,
,故
 ,
,从而
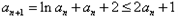 ,
,∴
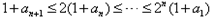 ,
,即
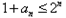 ,
,∴
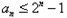 。
。 
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 .
. .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.