题目内容
(本题满分12分)已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点.
(Ⅰ)求实数m的取值范围;
(Ⅱ)求以PQ为直径且过坐标原点的圆的方程.
【答案】
解:(Ⅰ)
(法一)圆C: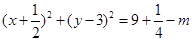 ,圆心
,圆心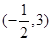 ,半径
,半径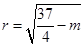
圆心到直线的距离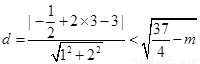 ,得
,得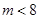 ;(4分)
;(4分)
(法二)由 ,有
,有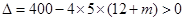 ,得m<8;(或者联立得
,得m<8;(或者联立得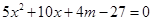 )(4分)
)(4分)
(Ⅱ)设P(x1,y1),
Q(x2,y2),由
∴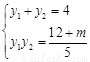
由于以PQ为直径的圆过原点,∴OP⊥OQ, ∴x1x2+y1y2=0,
而x1x2=9-6(y1+y2)+4y1y2= 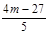 ,∴
,∴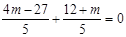 解得m=3.(8分)
解得m=3.(8分)
故P(1,1), Q(-3,3),圆的方程为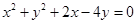 ,即
,即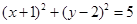 .(12分)
.(12分)
(法二)设过PQ的圆的方程为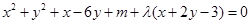
∴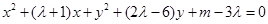 ,
,
即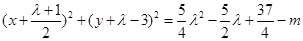
∵圆过原点,∴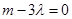 ,又以PQ为直径,则
,又以PQ为直径,则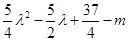 取最小值,此时
取最小值,此时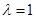 ,故m=3,圆的方程为
,故m=3,圆的方程为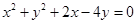 ,即
,即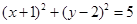 .(12分)
.(12分)
【解析】略

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围